A kezdeti és a központi pillanatok folytonos valószínűségi változó, ferdeség és csúcsossága

Home | Rólunk | visszacsatolás
Az alkalmazott problémák, mint például a több száz matematikai tistike, az elméleti tanulmány empirikus eloszlás részlegeik, eltér a normális eloszlás, a WHO-felmerül az igény mennyiségi becslések ezeket a különbségeket. Erre a célra, mi vezetett különleges dimenzió jellemzőit.
Opredelenie.Moda folytonos valószínűségi változó (Mo (X)) - ez a legvalószínűbb érték, amelyre a valószínűsége pi vagy valószínűség-sűrűség f (x) maximumot ér el.
Opredelenie.Mediana folytonos véletlen X változó (Me (X)) - ez az értéke, amely megfelel a következő egyenletet:
P (X
Geometriailag egy függőleges vonalat X = Me a (X) osztja a görbe alatti terület alakja két egyenlő részre.
X pontban = Me (X), a F eloszlásfüggvény (Me (X)) =
Find divat Mo, Me medián M és a várakozás egy véletlen X változó a valószínűség-sűrűség az f (x) = 3x 2. x Î [0; 1].
1. A valószínűség-sűrűség f (x) van maximuma az x = 1, azaz a f (1) = 3, tehát, Mo (X) = 1, az [0; 1].
2. Annak megállapítására, a medián jelöli Me (X) = b.
Mivel Me (X) megfelel annak a feltételnek a P (X akkor P (-∞ b = 3; b = »0,79 3. megjegyzés az eredő érték Mo (X), Me (X), M (X) a tengelyen Ox: Opredelenie.Asimmetriey elméleti eloszlás az arány a harmadik központi pillanata érdekében egy percet, hogy a kocka a szórás: Opredelenie.Ekstsessom elméleti eloszlást az úgynevezett on-érték határozza meg a következő egyenletet: ahol # 8210; középpontja a negyedik rend. Normális eloszlás. Amikor eltérés, eltekintve a normális eloszlás aszimmetria pozitív, ha a „hosszú” és a laposabb része a eloszlási görbe jobbra a pont az abszcisszán megfelelő vezetőképes módban; ha ezt a részét a görbe balra, a divat, az aszimmetria negatív (1A., b).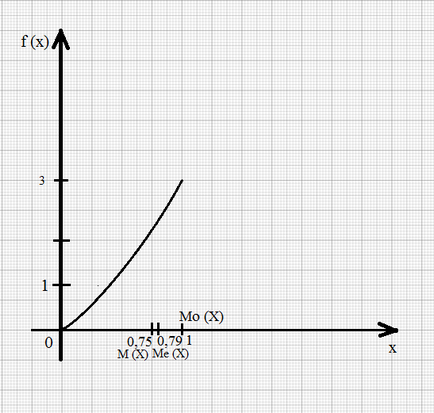
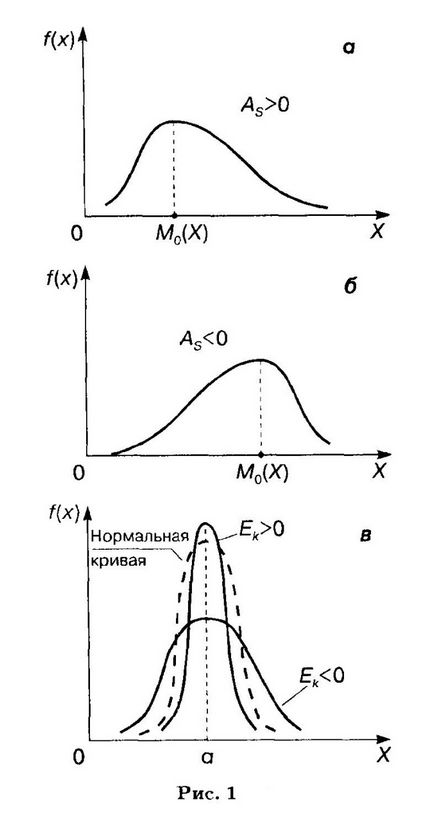
Csúcsosság jellemzi a „meredeksége” a görbe emelkedése az eloszlás a hasadási összehasonlítva a normál görbe, ha kurtosis polo-lakosok, a görbe egy magas és éles csúcs; esetén negatív kurtosis görbe hogy megfeleljen, és van egy alsó ferde tetején.
Belátható, hogy segítségével az összehasonlítás az említett referencia jellemzői hasonlóak feltételezéseket értékek matematikai elvárás és dis-persa normál és elméleti eloszlások.
Példa. Legyen egy diszkrét X valószínűségi változó adott eloszlás jog:
Keresés: ferdesége és csúcsossága az elméleti eloszlás.
Először megtalálják a várakozás SLE-véletlen változó:
Ezután kiszámítjuk a kezdeti és a központi pillanatok 2, 3 és 4-ed rendű, és a standard eltérés:
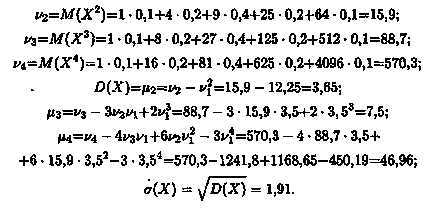
Most azt látjuk, képletek a szükséges ólom-fokozat:
Ebben az esetben a „hossz” az eloszlási görbe a verseny terített a jogot, a divat, a görbe önmagában nem-sokkal csúcsos, mint a normál görbe ugyanazokat az értékeket a matematikai várható értéke és szórása.
Tétel. Egy tetszőleges X valószínűségi változó, és bármilyen számú
# 1296;> 0 a egyenlőtlenségeket:
# 8210; a valószínűsége, hogy a szemközti egyenlőtlenség.
Legyen X -Expenses vizet, a haszonállatok (n).
A hipotézis, M (X) = 1000.
Ez nem kevesebb, mint 0,96.
A binomiális eloszlás Csebisev egyenlőtlenség formáját ölti: