A hatékony felülete az antenna nyílás, radiouniverse
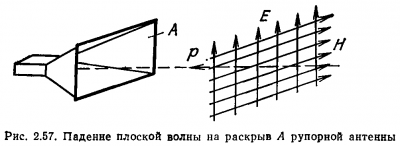
Trappable antenna teljesítmény függ olyan paramétereket, mint a nyílás területe (rekesz) az antenna. Annak érdekében, hogy jobban megértsék magukat ezt a kifejezést, képzeljük el a vevőantenna formájában kürt antenna amelyen síkhullámú (ábra. 2,57). Ha ez az étel is felszívja az összes hálózati esemény nyitó (rekesz), a hatalom az antenna által vett, egyenlő lenne $$ \ beginP = pA \ end \ tag $$
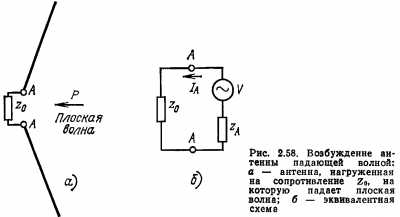
Beeső az antenna nyílás elektromágneses hullám gerjeszti az antenna bemeneti impedancia ZA = RA + IXa elektromotoros erő V. rész antennával vett teljesítmény kerül a vevő, amelynek bemeneti impedancia Z0 = R0 + iX0 (ábra. 2,58). Ezután az áram a vevő csatlakozik az antenna, $$ \ beginI_A = \ frac \ end \ tag $$ és a termelt villamos energia a vevő $$ \ beginP_0 = I_A ^ 2R_0 = \ frac \ end \ tag $$
Csak azt mutatják, hogy a maximális teljesítmény keletkezik a vevő megfelel a impedanciaillesztési feltétel, amely szerint RA = R0 és X0 = -HA.
\ End \ tag $$
Veszteségmentes antenna (Rp = 0) általános képlet szerinti (2.136) RA = Rizl. Ezután teljesen egyetért, azaz a. E. Amikor R0 = Rizl kapjunk a képlet a maximális érték a tényleges nyílás területe $$ \ beginA _ = \ frac> = \ frac\ End \ tag $$
Táblázat. 2.4 ábra értékeit Aeff max bizonyos típusú antennák.
Az igazi antennák Aeff max értéke mindig kisebb fizikai terület az antenna nyílás. Ahhoz, hogy értékelje a hatásos felületét az antenna nyílás bevezette a fogalmat felülete kihasználtsága a nyílás, amely az arány a hatásos felületét az antenna nyílás a fizikai terület az apertúra: $$ \ beginK _ = \ frac >> \ end \ tag $$
A maximális értéke a felület kihasználtsága eléri nyílást (az ideális antennák) = 1 értékek forráspont. Nagyon jó ár-érték antennák felület kihasználtsága esetén eléri a 0,7. 0.8.
IA áram az antenna sugárzási ellenállása RA egy áramforrása sugározzuk hullámok $$ \ beginP_ = I_A ^ 2R_A \ end \ tag $$
Az arány a teljesítmény sugározzuk antennát a teljesítménysűrűség incidens antenna o nyitott. meghatározza azt a területet reradiation (szórási rekesz) Aras. $$ \ beginA _ = \ frac>= \ Frac \ end \ tag $$
A rövid antenna teljes mértékben összhangban áll az incidens területen Aras Aeff = max. Amikor az antenna mismatch $$ \ kezdődik \ alpha _ = \ frac >> \ end \ kulcsszó $$ ahol αras ≤ 1.
Ha elvesztése ellenállás Rp> 0, a részét a felszabaduló energia az antenna formájában hőenergia. Lehetőség van, hogy a koncepció az autópályadíj plaza $$ \ beginA _ = \ frac\ End \ tag $$
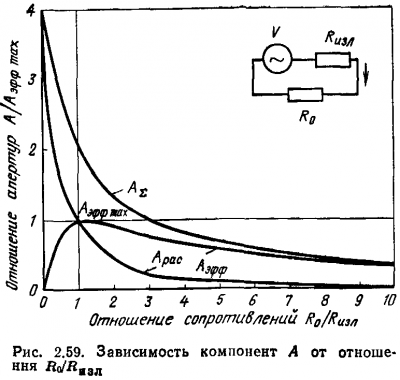
Ábra. 2,59 ábra grafikon az egyes komponensek An és AΣ teljes nyílásának arány R0 / Rizl ellenállás.
Van egy osztály a nyílás antennák. Ezek az antennák parabola antennák (itt a rekesz - nyílás tükör) tölcsérantenna (rekesz - megnyitása a hangszóró), stb
Az egység a nyílás lehet szögletes vagy négyzetméterenként, vagy a λ 2.
Hasznosítási arány a nyílás felülete határozza meg az (2.148).
Osztályú apertúra antennák Ki n <1, но для некоторых типов антенн значение этой величины может и превышать 1. К последним относятся антенны поверхностной волны и большинство проволочных антенн.
A kapcsolat a hatásos felületét Aeff nyílás. irányított együtthatója D és a hossza λ háború arányként $$ \ beginA _ = \ frac \ end \ tag $$
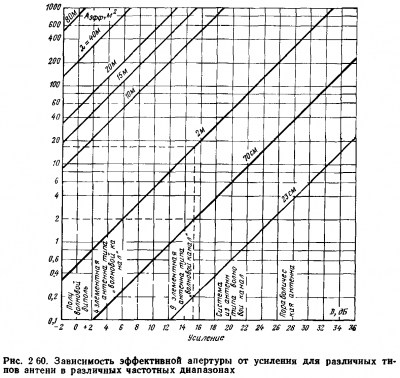
Ábra. 2,60 ábra grafikonokat Aeff (D. λ). A kapcsolat a Aeff és a szélessége a iránykarakterisztikának két síkban, és αE αH állítható egyenlet felhasználásával (2.128).
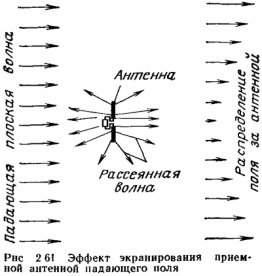
A vevőantenna felszívó az elektromágneses mező becsapódáskor által az elektromágneses hullám egyfajta képernyő a rádióhullámok. Ábra. 2.61 ábra vázlatosan mutatja a tér eloszlása a vevőantennát.
Az ábra azt mutatja, hogy közvetlenül azután, vevőantenna elektromágneses térerő csökken.
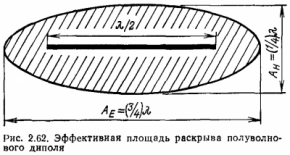
A félhullámú dipólus tényleges nyílás terület egy ellipszis (ábra. 2,62) a nagytengely AE = 3λ / 4 és kistengelye AH = λ / 4.
A felületi hullámok antennák, például antennák Uda - Yagi, a kapcsolat a lineáris méretei a nyílás, és a hatásos szélességük az antenna minta a két fő síkok és αE αH vannak létrehozott kapcsolatok $$ \ beginA_E = 2 \ sqrt \ alpha_E >> \ end \ tag $$ $ $ \ beginA_H = 2 \ sqrt \ alpha_H >> \ end \ tag $$
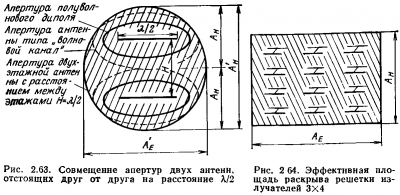
Ha két vagy több elemi antennák vannak elhelyezve egymás közelében (például, az egyik a másik felett, ábra. 2,63), majd a veszteségek csökkentésére kapott nyereségű antenna rendszer megköveteli, hogy a hatásos felületét apertúrájának részleges antenna elemek ne fedjék át egymást. Legelőnyösebben a jelen esetben, a pozicionáló elemek az antenna rendszert úgy, hogy a széleit a részleges hatásos felületű a nyílás érintkezésbe egymással.
A rács keresztirányú sugárzást kibocsátók (ábra. 2,64) lineáris méretei a hatékony felülete nyílásának egy elem van képletek alapján számítandó $$ \ beginA_E = \ sqrt \ alpha_E >> \ end \ kulcsszó $$ $$ \ beginA_H = \ sqrt \ alpha_H >> \ end \ tag $$
Összehasonlítása képletek (2.156) és (2.157) azt jelzi, hogy az utóbbi esetben a lineáris méretei a tényleges nyílás területe körülbelül 12% -kal kevesebb, mint amikor ezeket ugyanazokat az elemeket egy hosszanti emissziós antennák. Tekintsük néhány példát.
Példa 1. A terminálok a vevőantenna konfigurálva félhullámú dipólus részesülő rádióhullámok hullámhosszú λ = 2 m, és felvittük az ellenállás R0 = Rizl = 73 ohm kiszabott UA feszültség = 0,1 mV. Szükséges „kiszámításához a sugárzási teljesítmény állomás található a parttól r = 100 km-re a vevőantenna, azzal a megkötéssel, hogy, mint egy adóantenna használt félhullámú dipólus, és mindkét antennák orientált egymáshoz maxima mintákat.
1. A elektromotoros erő a kimenetén a vevőantennát V = 2UA = 2 · 0,1 · 10 -3 = 2 × 10 -4 V.
2. A tényleges nyílás terület egy félhullámú dipólus (lásd. Táblázat 2.4.) Aeff = 0,13λ 2 = 0,13 · 2 2 = 0,52 m 2.
3. A teljesítménysűrűség a helyét a vevőantenna p = V 2 / 4AeffRizl = (2 × 10 -4) 2/4 · 0,52 · 73 = 2,63 × 10 -10 W / m 2.
4. erőátviteli antenna sugárzási Pizl = 4πr 2 p / G = 4π (100 x 10 3) 2 · 2,63 · 10 -10 / 1,64 = 20,1 Watt.
2. példa beamwidth Yagi-Uda antenna hullámhosszon működtetve λ = 2 m, a αE = 25 ° és αH = 35 °. Ez az antenna be van töltve a következetes ellenállás R0 = 75 ohm. A teljesítménysűrűség az elektromágneses mező beeső antenna p = 2,63 × 10 -10 W / m 2 szükséges, hogy meghatározzuk a feszültség a kimeneti kapcsokon az antenna.
1. A nomogram ábrán látható. 2,54, a megadott értékeket αE = 25 ° és αH = 35 ° meghatározza az antenna nyereség G = 15, l dB.
2. A ábrán mutatjuk be. 2,60, ismert értékek G = 15, l dB és α = 2 m meghatározzák Aeff = 16,5 m 2.
4. A feszültség az antenna kimeneti UA = V / 2 = 0,56 mV.
3. példa kell számítani a távolságot H emeletek közötti emeletes Uda antennák - Yagi, ahol a sugárzási mintázat kerül megvalósításra, amelynek szélessége 25 αE = 0 és αH = = 35 °, és az antenna nyereség maximális.
1. A ábrán mutatjuk be. 2,60, a megadott értékek és αE αH. Mi határozza meg a hatékony terület Aeff = 4,5λ rekesz 2.
3. Ha az emeletek közötti távolságot antenna emeletes H = 2,8λ kapjunk maximális erősítést, amely, mint már tudjuk, megvalósul a feltétellel, hogy a nyílás széle hatásos felületű mindkét antenna elemek érintkeznek egymással.
4. hullámhossz λ = 2 m keresett távolság H = 5,6 m.
Megjegyezzük, hogy a megduplázása antenna nyílás vezet megduplázása nyereség (3 dB).
A számításhoz a rádiókommunikációs bevezeti a csillapítási tényező δ: $$ \ begin \ delta = \ frac> = \ fracA _ >> \ end \ tag $$ ahol PA - teljesítmény érkezett az antennát, amelynek tényleges nagysága Aeff nyílás oda; Pizl - által kisugárzott A sugárzó antenna, amelynek tényleges nagysága Aeff nyílás sáv; r - a távolság az adó és vevőantenna, m; λ - a hullámhossz, m.Formula (2.158) kapjuk az a feltételezés, hogy az antenna veszteségek nem orientált egymáshoz képest is, és azt is feltéve, hogy a távolság közöttük $$ \ beginr \ geq \ frac \ end \ tag $$ ahol d - a legnagyobb lineáris méret antenna; λ - hullámhossz.
Abban az esetben, ha a rádióhullámok utaznak a felszín közelében a föld, továbbá fennáll a közvetlen hullám és a visszavert hullám. Az eredmény a kölcsönhatás ezen két hullám az, hogy megváltoztatjuk a nagysága δ, számított képlet (2.158). A tényleges érték a csillapítási tényező Dp változik 0 <δр <4δ.
Mi továbbra is vizsgálja példa.
4. példa Erőátviteli sugárzás félhullámú dipól antenna Pizl = 20,1 watt. Meg kell kiszámítani a termelt energia egy illesztett terhelés fogadására antennát, amikor R0 = 73 Ohm, és feltéve, hogy a sáv Aeff = 16,5 m 2 Aeff ave = 0,13 m 2 és λ = 2 m.
2. A feszültség a kimeneti kapcsokon az antenna $$ U = \ sqrt> = \ sqrt> \ cdot> = 0,53 \ cdot> In $$.Az olvasó figyelmét arra a tényre, hogy néha a teljesítmény decibelben, és a szint 0 dB felel meg erejét 1W.