a folyadék kiáramlását a lyukakon keresztül
a folyadék kiáramlását a lyukakon keresztül
folyadék áramlása a nyílások, a vékony falat
Először azt kell tisztázni - mi is - „egy lyuk a vékony falon.”

Így a lyukat kell tekinteni, ha vékony b <3d ,
ahol:
b - a vastagsága az érfal,
d - átmérő (vagy magassága) a nyílás.
Amellett, hogy a koncepció a lyukak a vékony falú fogalmának egy kis lyukat a falon is.
Kis nevezett nyílás egy vékony falat. ha a függőleges kiterjedése kisebb érték 0,1 ... 0,2 Nyomás:
ahol:
és - a magassága a nyílás (m);
H - nyomás értékét (m).
Amikor a folyadék áramlik ki a kis lyukak a vékony falat egy állandó fej v sebességgel, és a Q áramlási sebessége határozza meg képletek:
v = φ √ [2g (H + P1 / ρg - p2 / ρg)]. (A továbbiakban √ - gyökös jel);
ahol:
ρ - a folyadék sűrűsége;
ω - keresztmetszeti területe a lyukak;
és ji φ - és áramlási sebességének arányát, amelynek értéke határozza meg a feloldó táblákat. Részlet egy ilyen táblázatok az alábbiakban mutatjuk be.
Az együtthatók φ és μ kapcsolódnak a μ = φε. ahol ε - jet kompressziós tényező, amely képviseli a terület aránya a repülőgép a tömörített részben a nyílás területre.
Táblázat sebességi együtthatókat és a folyadék áramlását a nyílások
Típus nyílást a falban az edény és a folyékony kisülési feltételek
jet sebesség arány lehet kifejezni együttható a helyi ellenállási veszteségek képlet:
ahol:
α - a kinetikus energia együttható;
ξ - együtthatója a helyi ellenállást veszteségeket.
A lejárt a folyadékot a tartályból a légkör felé nyitott (p1 = p2 = p) képlet meghatározására a sebesség és a nyomás egyszerűsített:
Q = μω √ (2gH). (M 3 / s).
X és y koordinátákat pontok jet tengelyvonala (. 1. ábra) ebben az esetben kapcsolódó szerint:
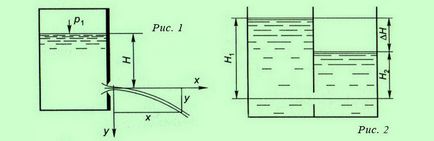
A lejárati egy réteg (ebben az esetben egy lyuk az úgynevezett elárasztott) és az áramlási sebesség által kifejezett az alábbi összefüggést:
Q = μω √ (2gΔH). (M 3 / s),
ahol: AH - a szintkülönbség (lásd 2. ábra ..).
A részleges kiürítése a nyitott prizmás tartály nyílásán keresztül egy vékony fal, amelyre a nyomás változik H1 H2. Ez adja meg:
amely, amikor a H2 = 0 (teljes kiürülését a tartály) válik:
ahol:
Ω - keresztmetszete a tározó területén (m 2);
W - folyadék térfogatát az edényben a kezdeti időben t = 0 (m 3);
Q - a folyadék áramlását egy kis nyíláson ω területen egy fej H1. Q = μω √ (2gH1). (M 3 / s).
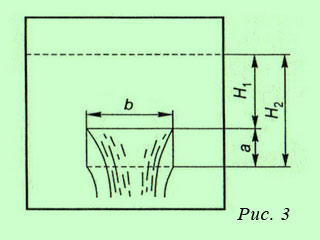
A lejárati nagy téglalap alakú nyílások a függőleges falon a tartály (. 3. ábra) a folyadék áramlását határozzák meg a képlet:
ahol:
b - a nyílás szélessége;
H2 - a nyomás felett az alsó nyílás széle;
H1 - a nyomás felső éle fölött a nyílás.