Mind a mikrokontroller
De a másik, nem kevésbé fontos, kérdés ( „Miért?”) Ebben a cikkben, a válasz nem. Általában az a benyomásom, hogy ez az író maga nincs egyértelmű válasz erre a kérdésre.
Remélem, hogy az érdeklődő olvasó megtalálja a választ ebben a cikkben.
Ahhoz, hogy megértsük ezt a kérdést úgy kell érteni, és a következő programozási témák: számrendszer, az alapokat a bináris aritmetikai és algebrai logika.
Hadd emlékeztessem önöket, hogy a 8-4-2-1 bináris kód a legtöbb MC. Folyton az 1. táblázatban minden bináris számok a táblázat négy bit, azaz Ők képviselik tetradból.
1. táblázat bináris kód 8-4-2-1
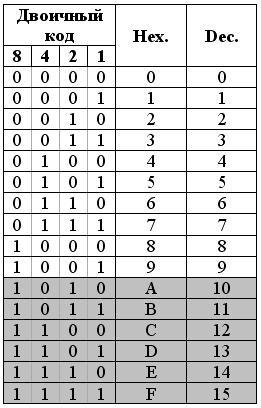
A kód 8-4-2-1 kódolható, mint egy 10-jegyű decimális számrendszer, és az összes 16 hexadecimális.
Ügyeljen arra, hogy a négyes szürkével kiemelve. Ezek a notebookok BCD nyilvánvalóan feleslegesek. Ezeket néha tiltott notebook vagy psevdotetradami. Amikor konvertáló bináris BCD tőlük (psevdotetrad) helyesen kell ártalmatlanítani. Ez az egyik kihívás ez az átalakulás.
Több kell adni, hogy a váltás egy bináris számot egy számjegyet (bit) balra egyenértékű megszorozzuk kettővel.
Példa: 1010 0111 = 167
Mi mozgathatja a bináris számmal kicsit balra, és kap kétszer annyi: 1 0100 1110 = 334.
Emlékezés mindezt, készen állunk a további vizsgálat bináris kód átalakítása BCD balra léptetés módszer.
Mi kell szem előtt tartani, hogy a BCD kód ne tartalmazzon psevdotetrad (lásd 1. táblázat ..), és ugyanarra a konverziós problémák közötti átadás tetradból 1, mindegyik - egy tizedes pontossággal.
Így, amikor mozog az egyik legfiatalabb BCD számjegy (tetradból) a következő magasabb rangú (következő szóval), a szám a „elveszett” egységek 6, mivel súlyozási tényező az ürítést 10 és egy bináris számrendszerben, és (túl és hexadecimális), akkor 16. Így áttevődik a bal oldalon a szám előállításához szükséges megfelelő korrekciós megszerezni a helyes eredményt.
Vegyünk egy tetszőleges nyolc bites bináris szám. Például: 11101101 (decimális ez egyenlő 237, és a hex - EDH). Akkor mi lesz „csúszik” egy bináris szám jobbról balra, az úgynevezett BCD bit rács, ezt a szükséges korrekciós átalakítani.
Az első három szám ebben a váltásban lehet „fájdalommentes”, korrekció nélkül. Az alsó számjegy BCD rács levelet a 7-es szám.
Ezután a negyedik váltás ez a kettős (ne feledjük, hogy a bal oldali sebességváltó - kettővel való szorzással) 1110 = 14
Kapott tilos négyes (psevdotetradu). By psevdotetrady, hogy „megszabaduljon”, szükség van hozzá a 6-os szám (110 bináris).
Ehhez 1110 + 110 = 10100 Emlékezzünk arra, hogy az így kapott szám - ez nem egy egyszerű bináris és bináris-decimális szám. A súlyozási tényező az MSB nem 16, és 10. Ezután a bináris-decimális szám 10100 megegyezik a decimális szám 14. A korrekciót.
A gyakorlatban egy sokkal kényelmesebb és sokoldalúbb módja korrekció. Ennek lényege, hogy a korrekciót elvégezni egészen a negyedik váltás, és csak akkor, ha szükséges. Az a tény, hogy ez már lehetséges megítélni biztosan kap a következő műszak psevdotetrada vagy utáni harmadik műszak. Hadd emlékeztessem önöket, hogy psevdotetrady merülnek fel nagy számban kilenc. Ez azt jelenti, ha a harmadik után váltás a három LSB egy bináris szám nem több, mint 4 (100), majd azt követően a következő műszak psevdotetrada jelenik meg. Psevdotetrady fordulhat elő, ha a negyedik előtt shift (azaz, mielőtt a következő szorzás 2) BCD rács lesz bármilyen számú ≥5 (101), mint a mi esetünkben, ez volt 7. végrehajtja a korrekciót, hogy a negyedik műszak szükséges:
- Ellenőrizze a számok az alsó három számjegy BCD rács.
- Ha ez kevesebb, mint 5, a korrekció hajtható végre.
- Ha ≥5 (101), akkor hozzá kell adni 3 (011).
Ez a harmadik esetben csak megfigyelni.
Elmentünk hozzá három, és hogy a 4. műszak.
Felhívjuk figyelmét, hogy a BCD rács után a 4. műszak mi volt a szám 10100, azaz 14, ugyanazt a számot, mint a felül 6 után a negyedik nyírási korrekciós módszerrel azt korábban tárgyaltuk.
Miért történik ez?
A válasz egyszerű. Amikor elhagyta váltás akkor megduplázva mint egy javított, és a korrekciós a (3 × 2 = 6). Egy matematikai szempontból egyenértékű módon.
Gyártunk az 5. váltás.
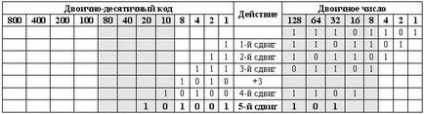
Megjegyzés fiatalabb majszol a BCD száma 1001 = 9, ami teljesen elfogadható. Felesleges BCD szám 101001 = 29. A következő műszak korrekció nélkül viszont számos 1.010.011 = 53, és legyen 29 × 2 = 58. Helyes felmerült hiba esetén lehetséges, mielőtt a váltás, hogy adjunk a műszakok száma „bűvös szám” 3.
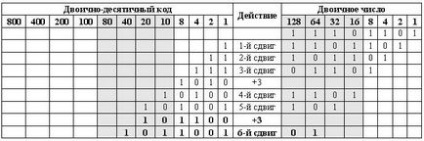
Egy új helyzetet. A LSnibble BCD száma „lefektetett” 9-es szám (1001), és a középső 5 (101), pontosabban 50 (lásd. A súlyok bitek ebben az évtizedben).
Ez azt jelenti, mielőtt a következő műszak szükséges, hogy a korrekció nemcsak LSnibble, de a következő átlag. hozzá kell adni a korrekciós LSnibble hozzá 3, és a korrekció az átlagos - 30, ahogy az az alábbiakban.
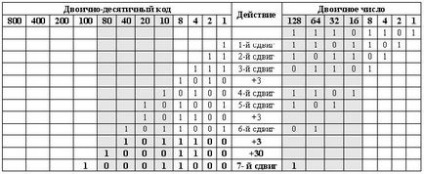
Most LSnibble az a szám, 8 (1000), ami azt jelenti, hogy a következő (utolsó) eltolódás hiányában korrekció 1 ugrás a következő tetrád, hogy teljesíti egy súlyozó tényező 10, 16 helyett, mint lenne egy hagyományos bináris számot. Ezért, mielőtt a 8. váltás LSnibble kell hozzá 3.
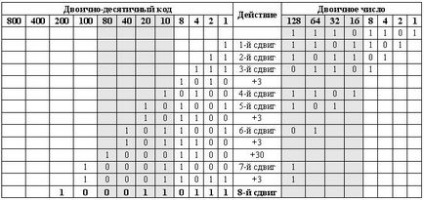
Konvertálása egy bináris szám BCD befejeződött. A bal oldalon megkapjuk a várt BCD háromjegyű decimális szám 237
(10 0011 0111), de ez a papír, legalábbis elméletben. Valódi mikrokontroller mindent hasonlít, de kicsit más. Legalább azért, mert a négy számjegyű (négy-) nyilvántartások nem léteznek, és minden BCD számjegy kiosztott teljes nyilvántartását. MC PIC átlagos család (és nem csak) ez egy nyolc számjegyű. A magas majszol e nyilvántartás mindig nullát (0000). Ez némileg megnehezíti az átalakulás algoritmus.
Felismerve ezt, tehát lényegesen könnyebb megérteni minden alprogram konvertáló bináris számokat decimális bináris balra léptetés módszer.
Az egyik legjobb, véleményem szerint, ezek a rutinok - egy univerzális rutin Alexei Cherepanov, amely megtalálható itt.