téglalap módszer - studopediya
Ezek részintervallumok épülnek téglalapok, magasságuk határozza meg az értéket a függvény f (x) bármely pontján alintervallumot.
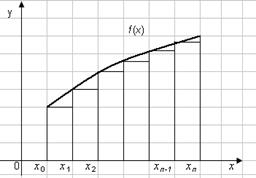
Ha f (xi) határozzuk meg a bal széle az egyes al-nyílásba (. 2.1 ábra), akkor a téglalap képlet a következő:
Ez az úgynevezett formula bal téglalapok.
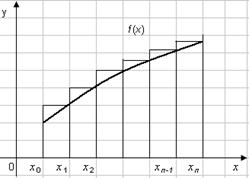
Ha f (xi) határozzuk meg a jobboldali határoló az egyes al-nyílásba (ábra. 2), a
Ez az úgynevezett formula a jobb dobozok.
Ha a funkció monoton intervallumon [a. b], majd egy esetben kapott szerves értéke I azzal a hátránnyal, I1. és a másik - feleslegével I2. A pontosabb értéket én kapott értékek átlagolásával:
Ha f (xi) határozzuk meg a közepén minden alintervallumot, a téglalap képlet a következő formában:
Ez az úgynevezett általános képletű átlagos téglalapok.
A pontosság az integráció e módszerek esetében közelítőleg egyenlő # 949; ≈ h.
A támogatás a bal, jobb és középső számítani téglalapok. Ha H = 0,2.
○ értékelése az integrál módszer téglalapok végre az Excel táblázatban (ábra. 3, 3-a).
Az értékek az integráció intervallum [0, 1], illetve elhelyezve a B3 és F3 sejt. Az integrációs intervallum van osztva részintervallumokra 5 (n = 5). Bemutatjuk az n értéke cellában B2. integrációs lépést vesszük a sejt F2 a képlet
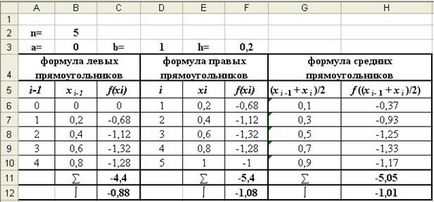
Ábra. 3 (megoldások mód)
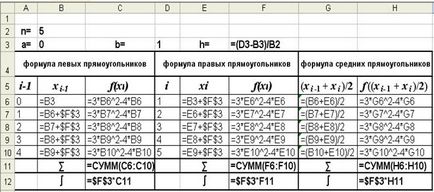
Formula megjelenítési mód
I) A közelítő kiszámítása az integrál a bal téglalapok (3) képletű kiszámításához szükséges értéke az f (x) = 3x 2 - 4x a pontokon (2):
Értékének kiszámítására x0. x1. x2. x3. x4. képviselte az elemi cellában B6: B10, és a megfelelő függvény értékei - a blokk sejtek C6: C10.
Majd kiszámítja ezek összege (a cellában C11), és a kapott értéket megszorozzuk integrációs H lépés (a C12 cella):
Σ = 0-0,68-1,12-1,32-1,28 = -4,4 I = 0,2 # 8729; (-0,44) = -0,88.
II) A közelítő kiszámítása az integrál alatt a jobb téglalapok képletű (4) kiszámításához szükséges értéke az f (x) = 3x 2 - 4x a pontot:
Értékének kiszámítására x1. x2. x3. x4. x5 képviselik E6 sejt blokk: E10, és a megfelelő függvény értékei - a blokk sejtek F6: F10.
Majd kiszámítja az összegük (cellában F11), és a kapott értéket megszorozzuk integrációs H lépés (a cella F12):
Egy hozzávetőleges értéke az integrál képlettel számítottuk ki a bal téglalapok egyenlő -0,88 és jobbra téglalapok képletű egyenlő -1,08.
A középérték közelebb a pontos egyenlő -1.
III) A közelítő kiszámítása az integrál másodlagos téglalapok a képlet (5) van szükség, hogy értékeit számítjuk ki az f (x) = 3x 2 - 4x a pontot:
(XI-1 + xi) / 2 (blokk G6 sejtek: H12), az összegük (H11-sejt), a kapott értéket megszorozzuk az integrációs lépés h (H12-sejt).
Felosztása az integrációs intervallum nagyobb számú szegmense, például, 10, kaphatnak pontosabb oldatot (4. ábra). # 9632 .;

Mivel a terület a trapéz felével egyenlő az összege az bázisok szorozva a magasság, az integrál megközelítőleg összegével egyenlő területek trapézok kapott:
Így, trapézok képlet formájában:
I = ≈. (8)
Integration pontossága ezzel a módszerrel körülbelül egyenlő # 949; ≈ H 2.
Példa (folytatás). # 9633; használata képletű trapézok értékeltük h = 0,2.
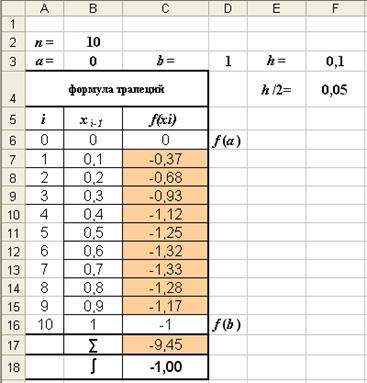
Határozat. Számítása az integrál trapezoid módszer (8) van az Excel táblázatban (ábra. 6, 6-a).
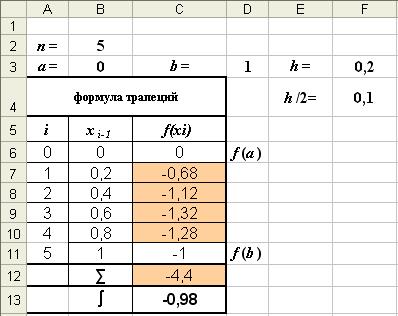
Σ = -0,68 -1,12 -1,32 -1,28 = -4,4 I = 0,1 · [(0-1) -2 · 4,4] = -0,98
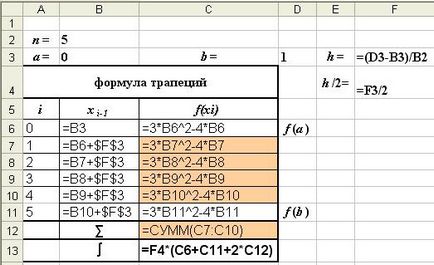
Formula megjelenítési mód
Felosztása az integrációs intervallum nagyobb számú szegmense, például, 10, kaphatnak pontosabb oldatot (ábra. 7).