Moment erő képest a pole
Vektor pillanata erő képest a pólus az úgynevezett vektor termék a sugár vektor és a erő vektor.
Az irányt a vektor erő pillanatban megtalálható a jobb oldali csavart szabály (ábra. 10). Mi át vektor
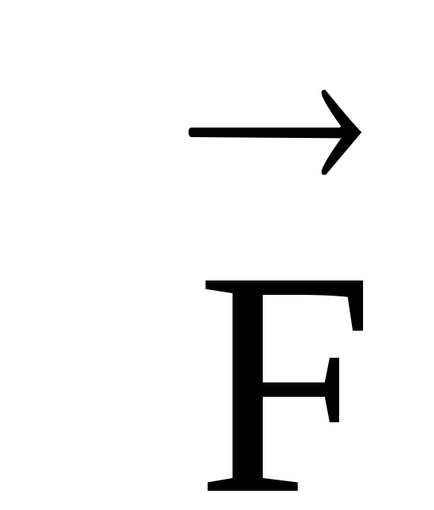
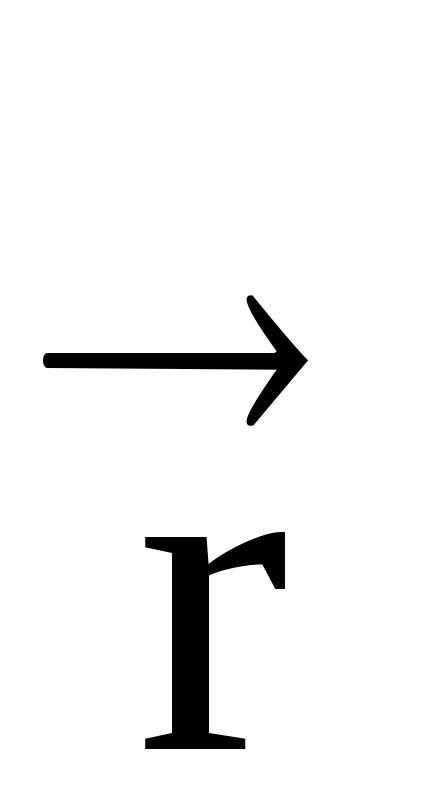
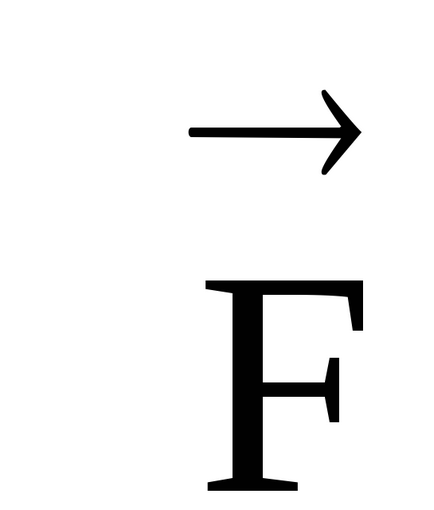
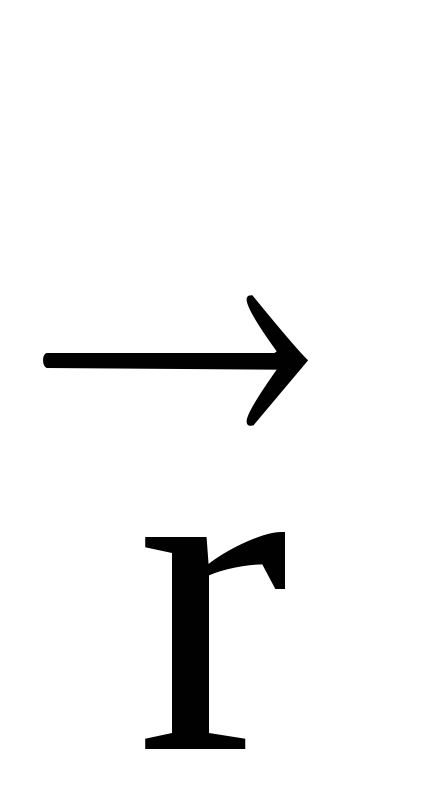
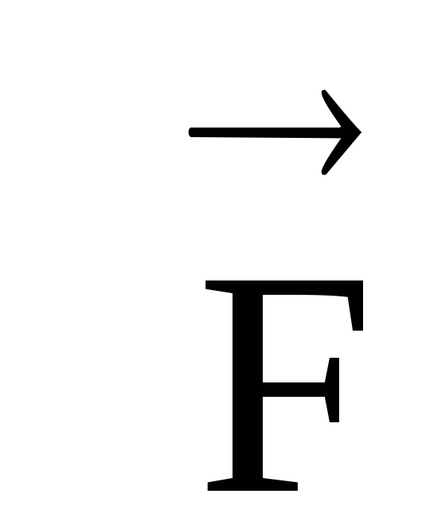
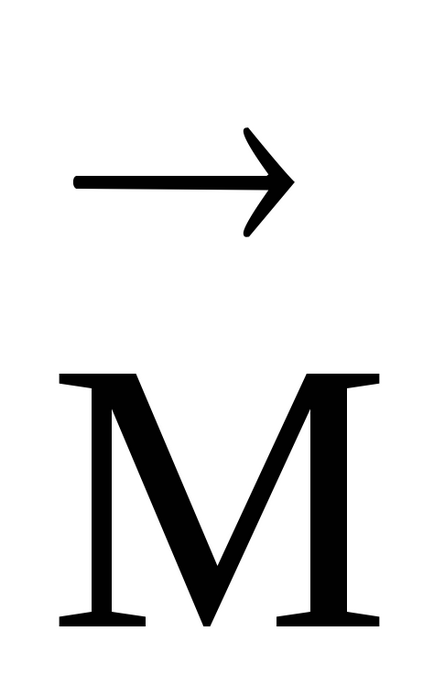
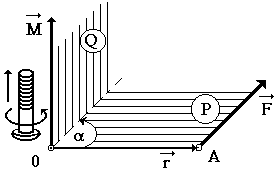
Megjegyzés. Abban az esetben, a vektor termék a vektorok
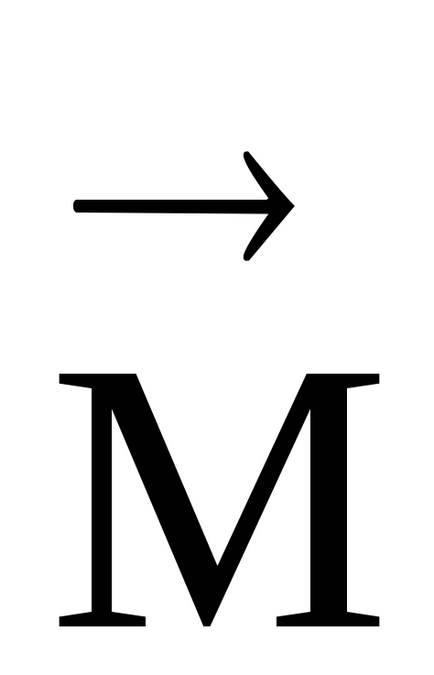
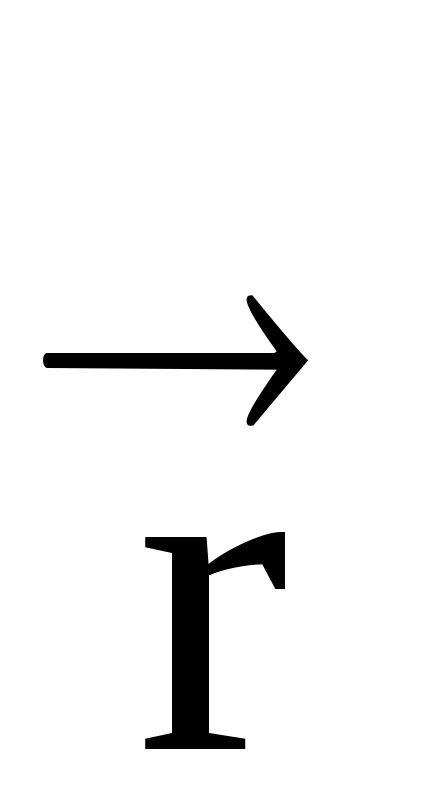
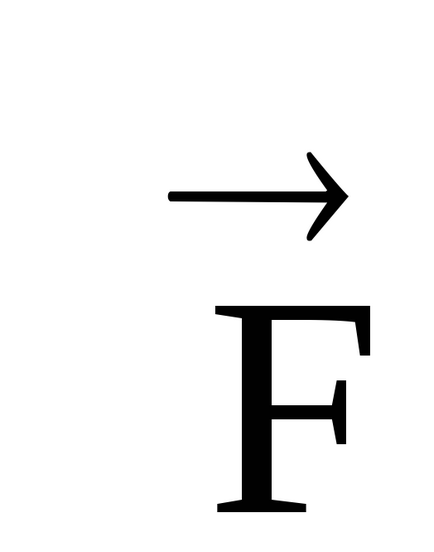
ahol
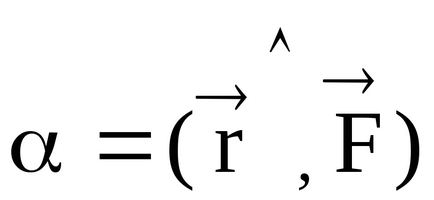
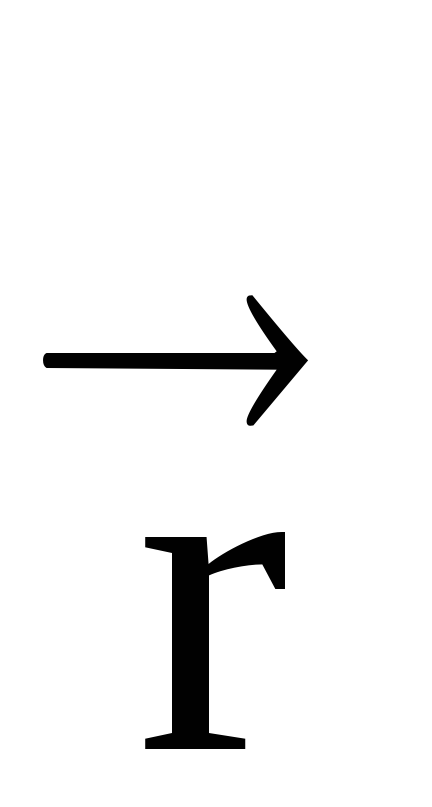
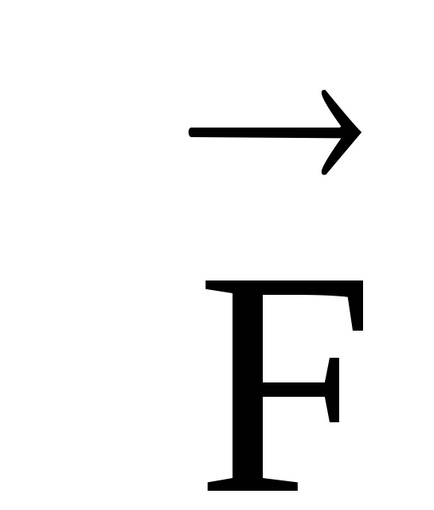
távolság
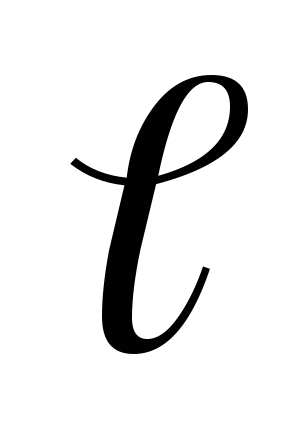
Bővítjük ható erő m t két részre ..:
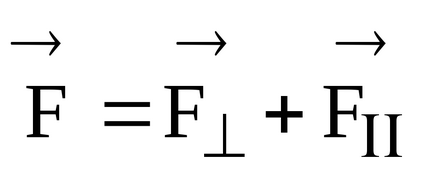
Ábra szerint. 11 nyomaték csak a hatalom
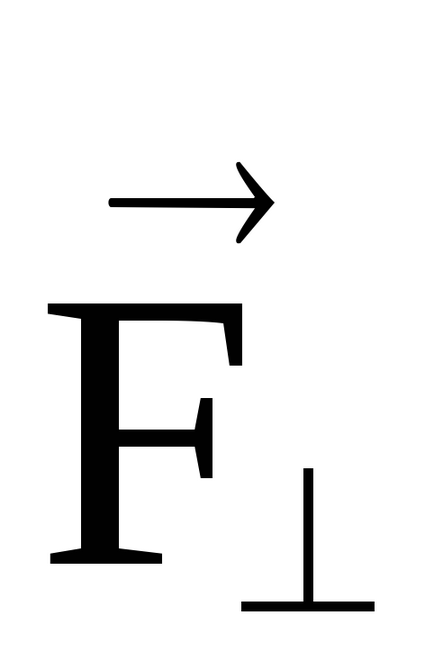
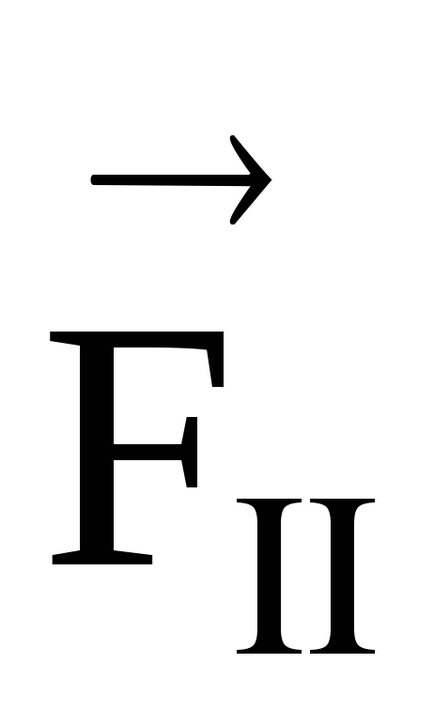
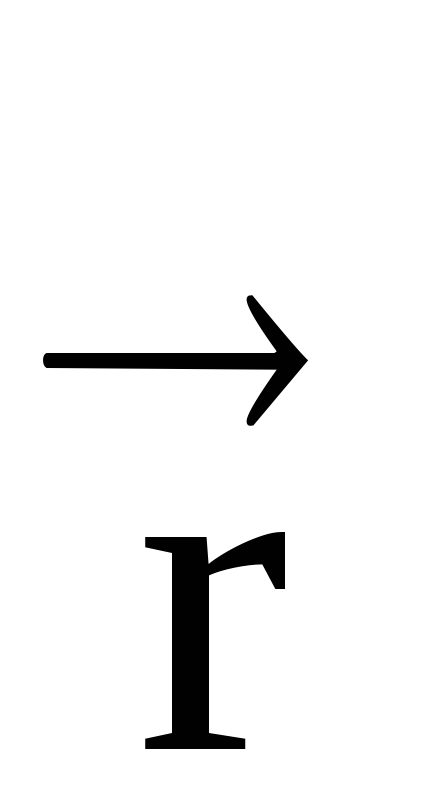
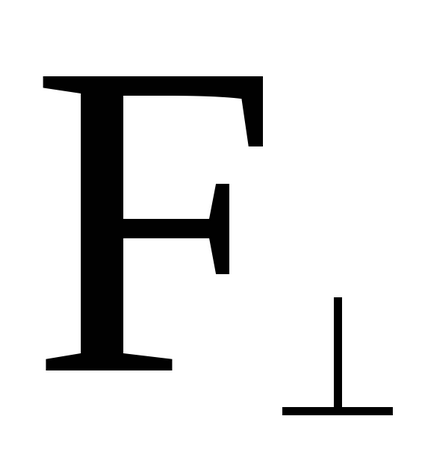
Vektor pillanatában hatályos
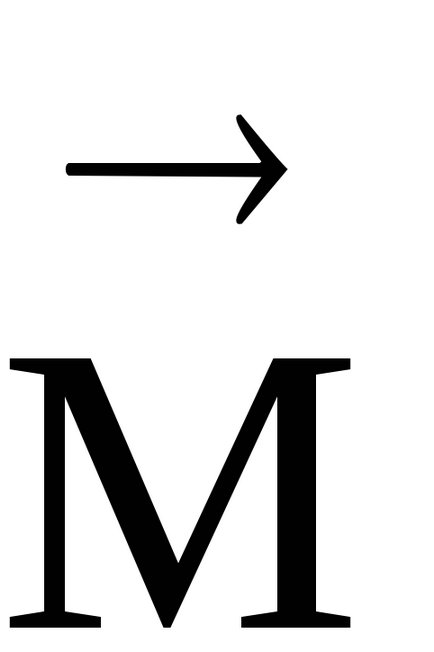
Az SI nyomatékot mérjük newton szorozva méter (Nm).
2.13. Abban a pillanatban, a kapott több erő
Ha m. R. (Body) egyszerre működik több erő, az eredő erő
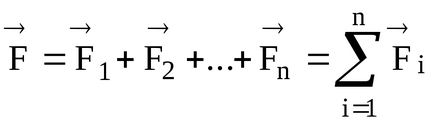
Moment vektor eredő erő képest a pole 0 ravengeometricheskoy vektor összege pillanatok összetevő erők viszonyítva ugyanolyan pole.
2.14. Pillanata pár
Egy pár erők említett két egyenlő nagyságú, de ellentétes irányú erő, nem fekszenek egy egyenes vonal.
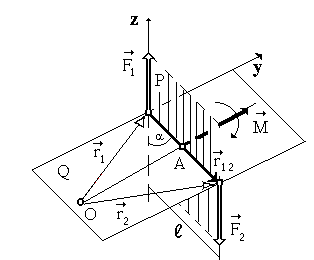
A definíció egy pár erők, ebből következik, hogy
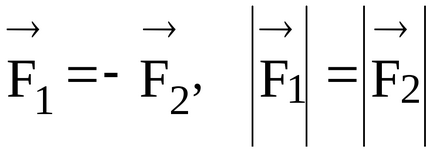
Ábra. 12, egy pár váll erőt
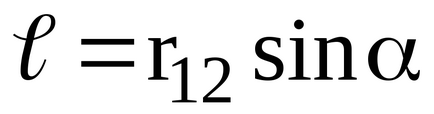
.
Az eredményül kapott nyomatéki
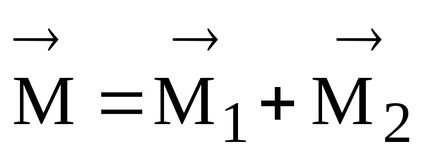
Ezután a pillanatban a két erő képest a pole 0 van írva, mint
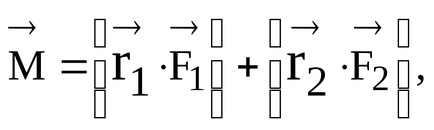
feltéve, hogy
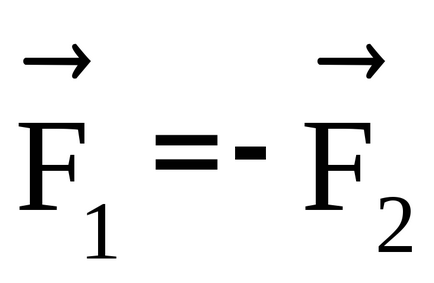
Pillanata vektor pár erők nem függ a helyzet a pólus 0.
2.15. Pillanatban a belső erők
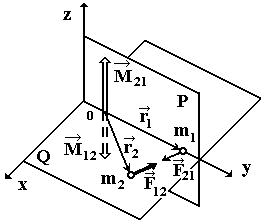
Egy példa a belső erők az erő a gravitációs kölcsönhatás a két vagy több részecske (szervezetek), vagy erejét a Coulomb kölcsönhatás töltött testek (részecskék) a zárt rendszer.
Ennek alapján Newton harmadik, ezek az erők egyenlő nagyságú és ellentétes irányú, és feküdjön ugyanabban a sorban a cselekvés (13.).
Sőt, mivel
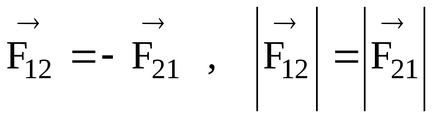
A viszonylagos nyomatékokat a belső erők az azonos pólusú (pont) 0 egyenlő nagyságú és ellentétes irányú:
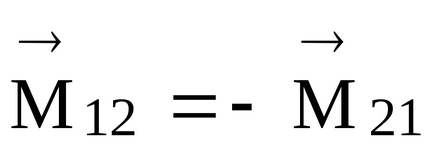
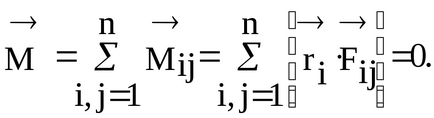
Megjegyzés. Abban az esetben, központi erő, amikor az irányok a vektorok a ható erők m. M. a rendszer átmegy egy rögzített pólus 0, a pillanatnyi erő mindig nulla (mivel a váll hiányzik).