Összefoglaló Karnaugh térkép
-
bevezetés
- 1 minimalizálás elvek
- 2 Leírás
- 3. példa
- 3.1 1. példa
- 3.2 Példa egy Karnaugh térkép öt változó
- 3.3 példa: a nagy Karnaugh Maps nyolc változók
Ábra. 1. példa Karnaugh Maps
Karnaugh térkép - grafikus minimalizálására kapcsoló (logikai érték) funkció segítségével viszonylag egyszerű művelet, nagy kifejezéseket és megszüntetése lehetséges versenyeken. Ez egy páros működése hiányos kötés és elemi felszívódását. Karnaugh térképek minősülnek megfelelően átépítették igazság táblázat funkciót. Karnaugh térképeket lehet tekinteni, mint egy adott sík dörzsár n-dimenziós Boole kocka.
Karnaugh térkép találták 1952-ben Edward W. Veitch és javított 1953-ban Maurice Karnaugh, fizikus a «Bell Labs», és úgy tervezték, hogy segít egyszerűsíteni a digitális áramköröket.
A Karnaugh térkép logikai változók továbbítja a igazság táblázat és elrendezve egy Gray-kód, amelyben az egymást követő szám abban különbözik az előző egyetlen bit.
1. Az elv a minimalizálás
Az alapvető eljárás minimalizálja logikai függvények képviseletében a PDNF SKNF vagy hiányos ragasztás páronként és elemi felszívódását. Működés párosított kötés nem jön létre a két kifejezés között (tag), amely ugyanazt a változót, amely (direkt és inverz) belépő ugyanaz az összes változót, kivéve egyet. Ebben az esetben az összes változót, egy kivételével, ki lehet venni a konzolok, a maradék zárójelben direkt és inverz előfordulása egy változó témában ragasztás. Például:
Hasonlóképpen, a CNF:
Az a lehetőség, felszívódás következik a nyilvánvaló egyenlőség
Így a fő cél, miközben minimalizálja PDNF és SKNF keresési kifejezések alkalmas ragasztás követő felszívódását, ami a nagy formák is nagy kihívást jelent. Karnaugh térképek nyújtanak intuitív módon, hogy megtalálják ezeket a feltételeket.
Mint ismeretes, a Boole-függvény N változók képviseletében a PDNF SKNF vagy állhat 2 N különböző kifejezéseket. Mindezek a tagok alkotják egy szerkezetet, topológiailag ekvivalens N n-dimenziós kocka, bármely két kifejezés, amely kapcsolódik egy él, ragasztásra alkalmasak, és felszívódását.
Az ábra azt mutatja, egy egyszerű igazság táblázat funkciójának két változó megfelelő ez a táblázat 2-dimenziós kocka (négyzet), és a 2-dimenziós kocka a kijelölése PDNF tagjai és megfelelő táblázatában csoportok kifejezések:
Abban az esetben függvényében három változó foglalkozni háromdimenziós kocka. Ez sokkal bonyolultabb és kevésbé átlátható, de ez technikailag lehetséges. Az ábra mutat példát egy igazság táblázat egy logikai függvény három változót és a megfelelő kockát.
Amint az ábrából látható, három-dimenziós esetben, bonyolultabb kifejezések konfiguráció. Például négy kifejezés tartozó egyik arca a kocka, egyesül egy kifejezés felszívódását két változó:
Általánosságban azt mondhatjuk, hogy a 2 K kifejezések tartozó K-dimenziós hypercube metszettel vannak ragasztva egy kifejezés, míg az elnyelt K változók.
legközelebbi alkalmas technikát javasolta, hogy egyszerűsítsék a munkát Boole-függvények számos változó. Cube képviselő struktúra szempontjából, zajlik a gépen ábrán látható módon. Így lehetővé válik, hogy képviselje Boole-függvények, több mint két változó formában sima asztalt. Emlékeztetni kell arra, hogy a sorrendben kifejezések a táblázatban kódok (00 01 11 10) megfelel a sorrendjét bináris számokat, és a sejteket a külső táblázat oszlopai, szomszédosak egymással.
Hasonlóképpen, akkor dolgozni a négy funkció öt vagy több változó. Példák a táblázatok N = 4 és N = 5 ábra mutatja. E táblázat kell arra, hogy a szomszédos cellák található megfelelő celláiban megfelelő oszlopok és a szélsőséges sejtek a felső és az alsó sorban. Asztalokhoz 5 és több változó figyelembe kell venni azt is, hogy a 4x4-es négyzet gyakorlatilag egymásra a harmadik dimenzióban, így megfelelő két szomszédos sejtek sosoednimi 4x4 terek, és a megfelelő feltételeket lehet ragasztott.
2. Leírás
Karnaugh térképet lehet tenni bármilyen változók számát, de kényelmes dolgozni a változók száma legfeljebb öt. Valójában Karnaugh térkép - egy igazság táblázat összeállított 2-dimenziós formában. Használata révén Gray-kód a felső sorban ez a fenék mellett, és a jobb oldali oszlopban szomszédos balra, ezáltal Karnaugh map minden gördült be alakja tórusz (fánk). Metszéspontjában a sor és oszlop elhelyezett megfelelő érték a igazság táblázat. Ha a kártya megtelt, akkor kezdődik, hogy minimalizáljuk.
Ha kell egy minimum DNP, a térkép csak azokat a sejteket, amelyek tartalmazzák az egységek szükség esetén CNF, majd úgy azokat a sejteket, amelyek tartalmazzák nullák. Minimalizálása önmagában szerint a következő szabályok (a példában DNF):
- összekapcsolják a szomszédos sejtek tartalmazó egységek a régióban, tehát, hogy az egyik régió tartalmazza 2 n (n egész szám értéke 0, ...) sejteket (emlékezzen a tény, hogy a szélsőséges sorok és oszlopok egymás mellett), a régióban ne legyen tartalmazó sejteket nullák
- régió szimmetrikusan kell tengely (ek) (a tengelyek vannak elrendezve, minden négy-sejtek);
- nem szomszédos területen szimmetrikusan elrendezett tengely (ek) lehet kombinálni egyetlen;
- területen olyan nagynak kell lennie, amennyire csak lehetséges, és a számos területen a lehető legkisebb legyen;
- A terület átléphető;
- több lehetséges opciókat fedez.
Következő, hogy az első régióban, és látni, hogy milyen változók nem változik ezen a területen belül, írja le az összefüggésben az említett változók, változatlan, ha a változó értéke nulla, bélyegzik meg inverzió. Vegyük a következő terület, végezze el ugyanazt, mint az első, és így tovább. D. minden területen. Kötőszavak területeken egyesítik eltérésre.
Például (a kártyák 2-ve változók):
CNF ugyanazokat a dolgokat, csak úgy, hogy a sejteket nullák, nem változik változók ugyanazon területen belül egyesítik a diszjunkció (inverzió nyomatni a egyváltozós), és a szétválás területeken összekapcsolják egymással összefüggésben. Ebben a minimalizálás befejezettnek tekinthető. Ennyit a Karnaugh térkép az 1. ábrán kifejezést DNF formátumban fog kinézni:
A CNF formátum:
Csak a DNF a CNF, és mehetsz vissza a de Morgan törvényeket.
3. Példák
3.1. 1. példa
A fiú Kohli egy anya, apa és a nagyszülők. Kohl sétálni az utcán, ha ő lenne megengedett legalább két rokonok.
Az egyszerűség kedvéért jelöljük a család Koli levélben:
Mom - x1
Apa - x2
nagyapja - x3
nagymama - x4
Egyetértünk jelölésére egység család beleegyezést nem járul hozzá nulla. Lehetőség sétálni betűvel jelöljük f, Nick megy sétálni - f = 1, Kohl nem megy sétálni - f = 0.
Construct igazság táblázat:
Pererisuem igazság táblázat egy 2-dimenziós nézet:
Átrendezzük azt a sorok és oszlopok szerint Gray-kód. Kapsz egy térképet Carnot:
Van egy igazság táblázat:
Karnaugh térkép fog kinézni (a jobb vizuális észlelés, a nullák nem írok a kártya):
Helytelen (a DNF például):
- - területe az S1 - fedett megfelelően;
- - Area S2 - ad 1. igénypont szerinti;
- - S3 Area - ad 2. igénypont;
- -S4 és S6 a terület - nem végez 3. igénypont, ez nem tévedés - minél több kifejezést, mint ha az S4 és S6 egy olyan terület;
- - Terület S5 - ad 1. igénypont száma sejtek és elfogadhatatlan a megállapítás a nullák a területen.
Ez igaz, de nem optimális:
Ez a térkép nem optimálisan minimális Carnot, mert akkor össze az egységek szerepelnek a S3 és S5 tagja.
Csökkentsük ezt a kártyát a következő DNF:
Elkészíti minimum CNF:
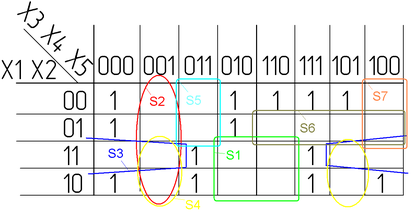
Egy másik változata az azonos Karnaugh Maps:
Semmi sem változik csak sorban három változót és két oszlopot.
3.3. Egy példa a nagy térképen Carnot nyolc változók
Tegyük fel, hogy a meglévő igazság táblázat össze ezt Karnaugh térképen:
Keressük a minimális DNF: