számítási komplexitás
Az összetett számítási eljárásokat - ez a fogalom a számítási komplexitás elmélet. a források értékelése (általában az idő) végrehajtásához szükséges az algoritmus.
meghatározás
Legyen - algoritmus megoldani egy osztály a problémák, és - a méret az egységes feladat ebben az osztályban. lehet, például a méret a feldolgozott tömb. Számoljuk meg a csúcsok száma feldolgozott, stb Jelöljük funkciót ad a felső határ a maximális számú alapvető műveletek (összeadás, szorzás, és t. D.), amelynek meg kell felelnie az algoritmus, a probléma megoldásának a dimenziót. Azt mondjuk, hogy egy polinomiális algoritmus A. ha nem gyorsabban nő, mint egy polinom. És különben is - exponenciális algoritmus.
Kiderült, hogy ezek között osztályok algoritmusok jelentős különbség: a túlméretezett a probléma (ami általában a legérdekesebb a gyakorlatban), többtagú algoritmusokat lehet végezni a modern számítógépek, míg az exponenciális algoritmusok gyakorlati dimenziója a probléma, mint általában, nem teljesülnek teljesen. Általában problémák megoldására generál exponenciális algoritmus társul egy teljes lista az összes lehetőséget, és figyelembe véve a gyakorlati lehetetlenségét ilyen stratégiát, hogy foglalkozzon velük kifejlesztett egy másik megközelítés.
Például, ha van egy exponenciális algoritmus az optimális megoldás a néhány probléma a gyakorlatban alkalmazni egyéb hatékonyabb polinomiális algoritmusok megállapítás nem feltétlenül a legjobb, de csak egy elfogadható megoldás (hozzávetőleges az optimális). De még ha a problémádra van megoldás segítségével egy polinomiális algoritmus, akkor csak az után épült egy mély megértése a probléma lényegét.
Polinom algoritmusok is nagyban függ a polinom foka, közelítő függőséget. Tekintsük az értékelés ideje összetettségét. Az ilyen értékelés végrehajtható a kapcsolatot ( „Big O”) azt mondják, hogy egyre növekvő nagy n és rögzített azt. Ha van egy pozitív konstans Const> 0 úgy, hogy. A becslés (g (N)) nevezzük aszimptotikus futási ideje.
Az értékelés során (g (n)) funkció akkor használható, ha a pontos érték nem ismert, és ismert, csak az eljárás növelésére fordított idő a döntést a dimenzió a probléma az N algoritmus A. A pontos értékek függnek a konkrét megvalósítására, míg O (g (n) ) egyik jellemzője az algoritmus. Például, ha az idő aszimptotikus összetettsége az algoritmus (Ilyen algoritmust nevezzük egy másodfokú), majd N növelésével megoldják a problémát növekszik, ahogy a négyzet a N. Az a tény, hogy az algoritmus a exponenciális komplexitás szempontjából beírt szimbólumokat lehet írva, mint. Amennyiben k - rendszerint egy egynél nagyobb egész.
Egy másik típusú értékelés társul bevezetése „alacsony”: azt mondják, hogy nem nő gyorsabban, mint a nagy N rögzítésre kerül. Ha. Például nyilvánvaló, hogy. Egy másik példa: van egy polinomiális algoritmus A if. Ahol P K (n) - a polinom foka N k. Így egy algoritmus komplexitása, amely aszimptotikus hogy (N log N), tárgya olyan polinom.
Példák aszimptotikus bonyodalmak
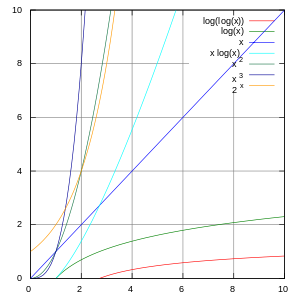
Grafikonok felsorolt funkciók a táblázatban.