Newton -módszer (érintők) - studopediya
Newton-módszer a leghatékonyabb módszer a nemlineáris egyenletek. Hagyja, hogy a gyökér. t. e .. Feltételezzük, hogy a függvény folytonos, és az intervallum kétszer folytonosan differenciálható az intervallumon. Let. Felhívjuk érintőlegesen a grafikon a ponton (ábra. 1.8).
érintőleges egyenlet lesz :.
Kapjuk első kereszteződés azáltal, hogy az abszcissza a metszéspontja az érintő a tengelyen. t. e. beállítást.
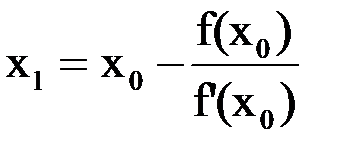
Ugyanígy járunk el a pontot. majd a m pont. g. Ennek eredményeképpen kapunk szekvenciát közelítések. és
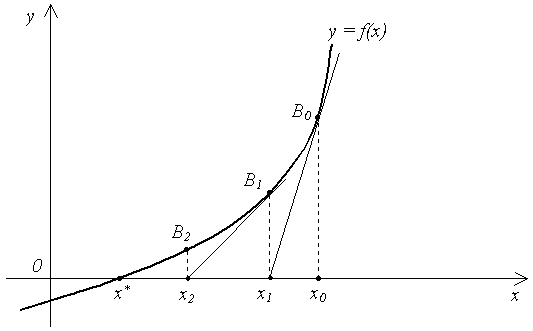
1.8 ábra - Az érintő a függvény grafikonját a ponton
Egyenlet (1.6) egy olyan számítási képlet a Newton módszer.
A Newton módszer lehet tekinteni, mint egy speciális esete az eljárás egyszerű iteráció amelyre
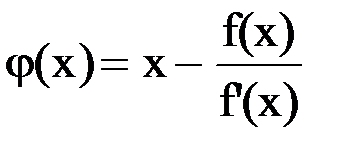
Módszer konvergenciáját. A konvergencia Newton-módszer meghatározza a következő tétel.
Tétel. Let - egyszerű gyökere az egyenlet a szomszédságában a gyökér függvény kétszer folytonosan differenciálható. Aztán van egy kis - gyökér környékén. hogy egy tetszőleges választás a közelítő értékét szomszédságában ezen iteratív szekvencia által meghatározott általános képletű (1,6) nem nyúlik túl ezen a környéken, és a becslés:
A konvergencia a Newton-módszer attól függ, hogy milyen közel van a gyökere az első megközelítésben kerül kiválasztásra.
A választás a kezdeti közelítés. Let - szegmens, amely a gyökér. Ha a kezdeti közelítés válasszon egyet a végpontok, amelyek. Az iterációs (1.6) konvergálnak, és monoton. 8. ábra megfelel az esetben, amikor a jobb oldali végén, a szegmens választották kezdeti becslés: (itt).
Hiba módszer. Becslés (1.7) kényelmetlen a gyakorlati alkalmazáshoz. A gyakorlatban az alábbi hibabecslése:
Megállás kritériumot. Értékelés (1.8) lehetővé teszi számunkra olyan az alábbi kritériumnak lezárását ismétléseket a Newton-módszer. Egy adott pontosságú számítást kell elvégezni, amíg egyenlőtlenség
.
1.3 példa. Newton-módszert kiszámítani a negatív gyökere az egyenlet 0,0001. Fürdőzés után egy ág gyökér, azt látjuk, hogy a gyökér lokalizálódik az intervallumban. Ebben az intervallumban. Mivel mind. Ezután a kezdeti közelítését lehet venni.
1.3 táblázat - Számított érték