Homomorfizmus és izomorfizmus algebrák - studopediya
Algebra különböző látszólag jelentősen eltérő struktúrákat. Ha az algebra azonos típusú, a jelenléte ezen hasonlóságok jellemzi alacsonyabb fogalmak bevezetett homomorfizmus és izomorfizmus.
Legyen adott két algebra
Az azonos típusú, vagyis és argumentumainak száma ..; és; és - ugyanaz.
Homomorfizmus az A a algebra a B a kijelző -. feltételeknek eleget:
minden (- argumentumainak száma és működését.
A jelentése (1) feltételt:
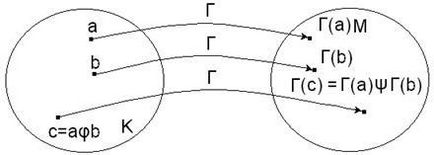
függetlenül a művelet a készlet K első végezni, és hogy a leképezés ezután előállított T vagy T leképezési először elő, majd a beállított M képződik megfelelő működését. az eredmény ugyanaz lesz.
Izomorfizmus az A-ra a algebra B nevezzük bijektív homomorfizmus. Ebben az esetben van egy inverz leképezés. mint egy-egy.
Let. . Aztán. Cseréje (1) bal oldalán ezen egyenletek jobb és alkalmazni mindkét oldalán a kapott egyenlet. Ettől. kapjuk:
(2) egyenlet - ugyanaz, mint az (1) egyenlet a csere a F. elemeit K készletben lévő elemek M és felcseréljük és. Más szóval - ez izomorfizmus B. A.
Ha van izomorfizmus az A-ra B. van egy izomorfizmus a B-A; ebben az esetben az A és B nevezzük izomorfak.
Power a fuvarozók izomorf halmazok (a homomorfizmus ez az egyenlet nem hajtható végre).
Automorfizmusa on sebyailiavtomorfizm - ez homomorfizmus azzal a megkötéssel, hogy A = B
Izomorfizmus a - izomorfizmus.
1. Tegyük fel, hogy - a készlet minden egész; - a készlet minden páros számok;
a) algebra és izomorfak. Izomorfizmus a feltérképezése. ahol az állapot (1) Itt a formája 2 (a + b) = 2a + 2b. Mert. akkor F - algebra izomorfizmus a.
b) térképezés egy algebra automor.
Feltételek (1) a formája:
c) mapping algebra nem automorfizmusa, mint
2. Egy közötti izomorfizmus algebrák és egy kijelzőt (- pozitív alcsoport R).
Feltételek (1) rendelkezik a forma egyenlet:
3. Boole-algebra Cantor B (U), A) és B (),), amely két, különböző készletek U és egyenlő teljesítmény izomorf. Műveletek ugyanúgy, és a kijelző bármelyike, a D egy-egy levelezés között U és.
Az arány izomorfizmus egy ekvivalencia reláció egy sor algebrák:
- reflexivitás izomorfizmus kapcsolat nyilvánvaló;
- szimmetria következik, hogy létezik a fordított izomorfizmus;
- tranzitivitás beállítása a következő: ha - izomorfizmussal B. A - izomorfizmus S. A izomorfizmus A-C és az akarat összetételét.
Ekvivalencia osztályok a partíció képest izomorfizmussal osztályok egymással izomorf algebrák. A koncepció a izomorfizmus - az egyik legfontosabb a matematikában. Ennek lényege, amint az a példákból lehet kifejezni: Ha A és B izomorf, az elemek és a műveletek B átnevezheti úgy, hogy a B egybeesik A.
(1) feltételt izomorfizmus az következik, hogy minden olyan ekvivalens aránya az A mentett bármely izomorf s algebra. Ez lehetővé teszi, hogy megkapjuk azokat a kapcsolatokat az algebra és automatikusan osztja azokat valamennyi algebra izomorf A. A közös matematikai kifejezés „tekinthető akár izomorfizmus” azt jelenti, hogy csak azokat az objektumok tulajdonságait, amelyek tárolják az izomorfizmus t. E. közös minden izomorf tárgyakat.
Különösen a izomorfizmus megőrzi asszociatív, kommutatív, elosztó.