Építőipari és átalakítása 3d grafika és tárgyak
Lab № 5
Tárgy: Építési és átalakítása 3D grafikát és egyéb terjedelmes tárgyak.
Cél: megismerni telek funkciók és különböző tárgyakat a térben, amelyet hallgatólagosan paraméteres formában, poláris koordináták és gömbi koordináták.
Feladat 1. rajzoló funkciókat az űrben.
Az ábrázoláshoz Z = f (x; y) használunk Plot3D funkciót. Ez adott a következő formákban:
Plot3D [f,<>,<>] - épít egy grafikon, a Z = f (x, y), mint x változik intervallum in-up;
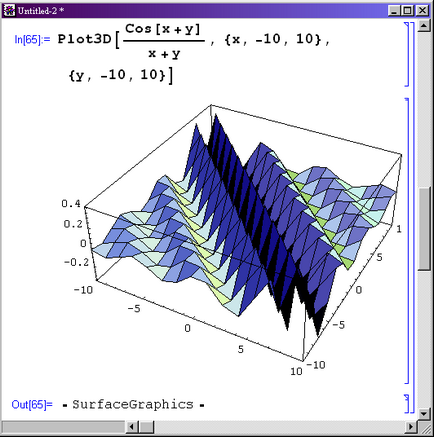
a) Ábrázoljuk a funkciója, mint x változó -10 10 és y változik -10 és 10.
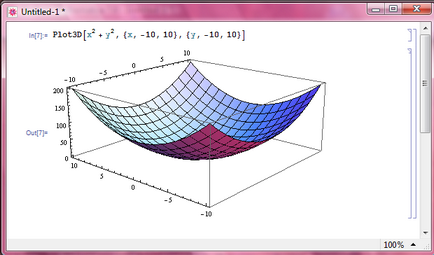
b) Ábrázoljuk a függvény z = x 2 + y 2 x változó -10 10, és y változó -10 10.
Construct grafikonok funkciók:
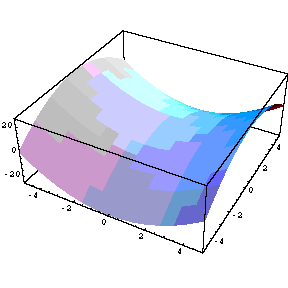
; ; . Z = sin (xy); x 3 + y 2 - Z 2 = 0.
Feladat 2. rajzoló funkciókat egy meghatározott térben parametrikusan.
Nem minden a felület lehet a következő egyenlet adja z = f (x, y)), vagy táblázatos formában. Gyakran sokkal könnyebb kérni őket parametrikusan. A paraméteres görbék is, meg a térben. Parametrikus meghatározott háromdimenziós térben vagy kétdimenziós felület háromdimenziós görbéket lehet levonni keresztül ParametricPlot3D funkciót.
Hívjon ParametricPlot3D [t. yt. ez], min. tmax>] visszatér térbeli görbe paraméteres változó kezdve Tmin a TMAH.
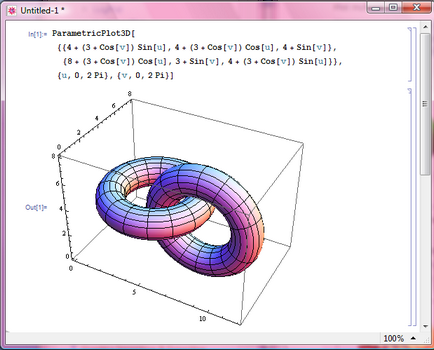
Építsen ugyanazon a grafikonon:
3. feladat Building 3Dgrafikov gömb koordinátarendszerben.
A funkció használatához a - a legegyszerűbb módja, hogy össze egy gömb. Ez természetes, hiszen a gömbi koordináta-rendszerben. És mi a gömbi koordináta-rendszerben nevezzük?
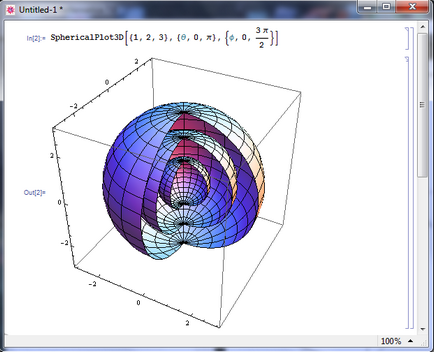
Ábrázolt függvények:
a) Y = 1+ (Sin (5U) / 5), és v 0 és tc, és u 0 és 2π;
b) Y = 1 + 2Cos (2u), ha u 0 és π, és v 0 és 2π.
Feladat 4. ábrák forgatást.
Széles körben elterjedtek a háromdimenziós grafikus objektumok görbék képest forgástengely körül. Például, a fordulási kör által szögben π, a labda felülete lehet beszerezni. Tartomány megváltoztatása variációs forgásszögön építhető nyitott vagy zárt formák. Hogy ilyen felületek (számok) a funkció Mathematica: RevolutionPlot3D [FZ, min, tmax>. ] És RevolutionPlot3D [x, fy, FZ>, min, tmax>. ].
Ábrázolt függvények:
a) Z = t 4 - t t 2. át 0-1;
Feladat 5. A különböző háromdimenziós tárgyak
Mathematica számos színes számok, tervezett formájában adatok példák (ExampleData). Ezeket fel lehet használni, hogy teszteljék a teljesítményét grafikus funkciókat. Ábra. Az 5. ábra a szerkezet egy volumetrikus alakja számos példát használva ListSurfacePlot funkciót. Csak olyan lehetőség, amely meghatározza a szilánkok száma számok. A többi opció alapértelmezés szerint.
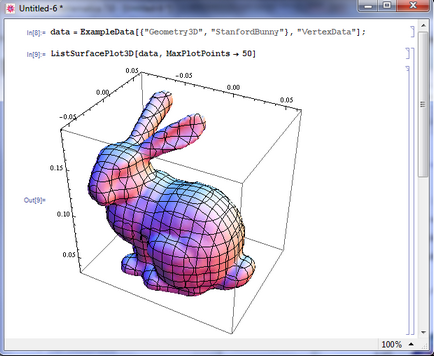
Construct image ábrán látható. 5, a:
6. Fontos feladat felülete (analitikus geometria a tér).
Ábrázolási térben óta használják a megszokott funkciót. ahol f - funkciója a változók x és y, ahol. .
Felrajzolásához egy második sorrendű felületet először kifejezni z változó a kanonikus egyenlet. Ezt meg lehet tenni a megoldásához funkció, amelyet már felhasználtak az egyenletek megoldására megadásával csak ismeretlen változót z. Például, tudjuk kifejezni egyenlet ellipszoid változó z:
Ez azt jelenti, hogy az építőiparban a ellipszoid csökkenti az építési azonos koordináta rendszert, és két háromdimenziós diagramok.
Mivel a grafika kell építeni az azonos koordinátarendszerben, akkor használja ezt a funkciót Show. Ezen túlmenően, az építési ütemterv céljára minőségének javítása grafikák segítségével PlotPoints opció -> n, ami azt jelzi, hogy hány részt kell venniük az építőiparban (n - természetes szám). Az opció Mesh -> False eltávolítja a felületi a hasított vonal, amely hozzájárul a prezentáció a képben.
Tedd magad minden egyes vizsgált példák. Változás paraméterek a, b, c, és állítsa be, ahogy növeli vagy csökkenti a hatást a kép felületén. Meg kell növelni vagy csökkenteni a tartomány a változókat.
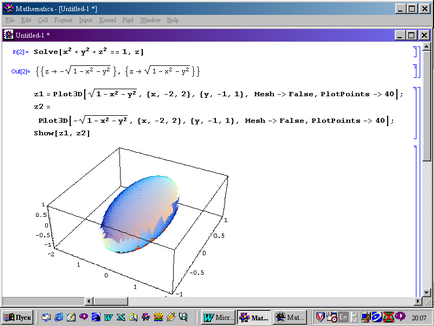
A 6. ábra a szerkezet egyenlet által definiált egy ellipszoid.
b) hiperboloid egy lap.
A 7. ábra a szerkezet, hiperboloid egy lap, egy előre meghatározott egyenletet.
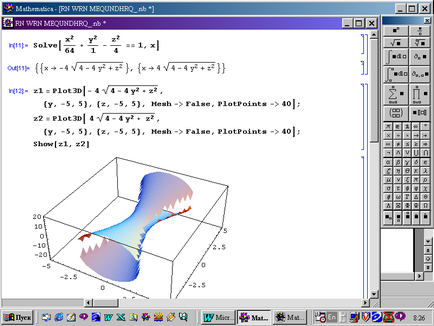
A 8. ábra a szerkezet a két lap alakú hiperboloid, egy előre meghatározott egyenletet.
Construct következő másodrendű felület:
a) A hiperbolikus paraboloid (kanonikus egyenlet) egyenlet által definiált.
b) elliptikus paraboloid (kanonikus egyenlet) egyenlet által definiált
c) egy elliptikus henger (kanonikus egyenlet) egyenlet által definiált.
d) A hiperbolikus henger (kanonikus egyenlet) egyenlet által definiált
e) A parabolikus henger (kanonikus egyenlet) egyenlet által definiált
f) Egy pár egymást metsző síkok (kanonikus egyenlet) egyenlet által definiált.
g) egy pár párhuzamos síkok (kanonikus egyenlet:
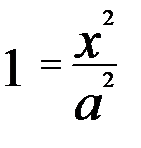
h) Egy pár átfedő síkok: a kanonikus egyenlet.
Feladat 7. Változás a szög.
Mathematica lehetővé teszi a felhasználó megtekintheti bármilyen beépített térbeli adatok különböző pozíciókban. Változtatni a térbeli helyzetét háromdimenziós alakzatokat 3D View Point választó lehetőséget. Ez az opció be lehet állítani a beviteli eszköztár. A kurzor kell tenni a tizedesvessző után, és állítsa be a záró zárójel.
A 9. ábrán látható egy példa segítségével ezt a lehetőséget.
Mi bemutassa a különböző pozíciók hiperbolikus paraboloid az űrben. A 10. ábrán be van építve használata nélkül lehetőségek a 11. ábrán annak alkalmazása.