Telhetetlen kecske, 5. évfolyam, bögrék, kis Mekhmat

Kecske - egy nagyon falánk állat. Esznek minden füvet, hogy ami elérheti. Ezért tartják pórázon. 1. Kösse a kecske a réten, hogy evett egy kört.

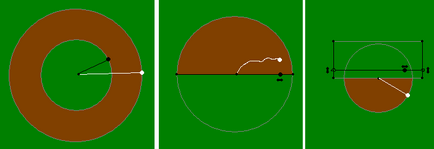
Válasz. Meg kell kötni, hogy egy kötéllel, amelynek hossza megegyezik a kör sugarát, és a csap állandó a közepén. Aztán, hogy túllépnek a kör, a kecske nem elég hosszú a kötél, hogy minden pontot a körön kívül eltávolítjuk a központtól, hogy a távolság nagyobb, mint a sugár (és így, mint a hossza a kötelet). Ezzel szemben, az összes pont egy körön helyezkedik el, nem messze a közepén, mint a sugár, így a kecske eszik mindent a körön belül.

2. Milyen része megeszi a kecskét, ha kötve két csapok? (A kötelet kötött a két pólus és kecske prodernuta a gallér.)

Válasz. Ő fog enni pontosan a szegmens, amelynek végpontjai vannak a csapok. Fogjuk bizonyítani, hogy ez így van. Sőt, a fű bármikor ebben az intervallumban is lehet enni; ha tudna többet enni füvet bármely pontján nem hazudik ebben az intervallumban, a kötél, amelyhez kapcsolódik, kellene nekifeszülünk, de azzal a feltétellel, a probléma meg van nyújtva, úgyhogy sehol máshol, hogy a kecske nem.

3. Rodion séta a réten, kezében egy kecske pórázon 1m. Útja egy téglalap oldalai 3 és 5 m. Mi rét föld megeszi a kecskét?

Megjegyzés. Ha nem tud azonnal megoldani a problémát, próbálkozzon poreshat pihenés, majd visszatérek rá. Javasoljuk, hogy nem ugyanaz mindig és minden más esetben.

Megjegyzés 2. Döntse első feladat №5.

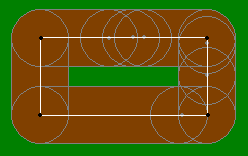
Válasz. A kör sugara körül 1m bármely pontján mindkét oldalán a téglalap minden lehet enni (ábra szemlélteti példák ilyen körök). A külső határ formák lesz négyszög lekerekített sarkokkal (nézi a rajz közelebb megérteni, hogy miért a görbületi sugár egyenlő 1m) és oldalán 3 + 1 + 1 = 5 és 5 + 1 + 1 = 7 méter. A belső határokon - ez egy szabályos téglalap oldalai 3 - 1 - 1 = 1 és 5 - 1 - 1 = 3 méter.

4. Tie kecske keresztül kötelek és csapok így lehetett füvet csak egy része ebben a formában:

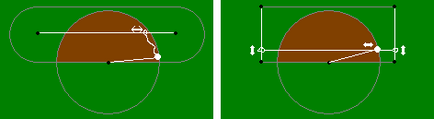
Válasz. Ez a terület - a kereszteződés két kört. Tie egy kecske az első feladat, így nem tudott kijutni az első fordulóban, a központ az első fordulóban egy karakterlánc, amelynek hossza megegyezik a kör sugara. Egyidejűleg egy másik nyakkendő kecske kötelet, amelynek hossza megegyezik a sugár a második kör, a közepén ez a kör. Ennek eredményeként, a kecske nem lesz képes kijutni az első fordulóban, mert kapcsolódik a központ és a második fordulóban, és mivel van kötve a közepén. Ez azt jelenti, hogy mindig kell elhelyezni a kereszteződésekben a két kör. (A meghatározás és a készletek átkelés minta itt található.)
Megjegyzés: általában a kecske nem jött a kereszteződés minden két, elég (bár nem feltétlenül, sőt lehet egy módja annak, hogy ennek eléréséhez más módon) lekötni úgy, hogy nem jön ki az első, és nem jön ki a második azaz, hogy megoldja a problémákat, két független.

5. húzza a kötelet rét két kampókat. A második kötél egyik végét kösse a gallér kecskék, míg a második fog tenni a hurok, szabadon mozgó mentén a kötelet. Mi telek vyest kecskét?

Válasz. Egy egyenlő távolság hossza a második kötél, minden pont az első kötél, mindent lehet enni. Így lesz kiűzni körök, amelyek középpontjai a kettő közötti időszak kampókat (ábra egy néhány példát az ilyen lemezek). A Union formák alakja, amely egy téglalap és két félkör (ez is lehet nevezni négyszög lekerekített sarkokkal, amelynek sugara a kerekítés egyenlő a szélessége a téglalap és a hossza a második kötél, és egy téglalap egyenlő hosszúságú első kötelet plusz kétszer a hossza a második kötél).

6. Tartsa kecske keresztül kötelek és kampók
a) félkörben;
b) a téren;
c) a téglalap (téglalap megoldott kétféleképpen).

Megjegyzés. Képzeld mindegyik számadatok a kereszteződésekben a két alak, amelyre egy hasonló probléma már megoldódott előtt. Ezen túlmenően, a négyzet és a téglalap is felér egy másik megoldást.

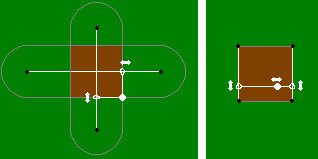
a) Először is, nyakkendő egy kecske úgy, hogy nem jön ki egy teljes kört. Mi kell hozzá több kötelet tartani a jobb oldalán. Ez a része a határ a félkör egy vonalszakasz, mint például a határon volt korábban a probléma 5. Ezért kötődnek neki tovább a leírt módon ezt a feladatot. Szóval, lehet képzelni, hogy egy félkör a kör metszéspontja és a darab, ami a probléma 5. Több helyettesíteni lehet a szám 5 téglalap.

b) tér - kereszteződés két darab 5 céltárgy, amelyre a második kötél hosszúságú azonos.

c) A téglalap is leírható, mint a kereszteződés két ilyen darab, de akkor jön egy másik kötelet rendszer, ahol a kötél csúszik csuklós két sínen, és a kecske van kötve vele a gallérját, hogy tudott sétálni a kötelet.

kutyák részt ezeket a feladatokat. Ezek befolyásolják a kecske is: a kecske nem megy oda, ahol a kutya is elérheti. De ezt a kecskét nem éhezik, tartson kutyát pórázon is. 7. Az egyik kutya hold kecske
a) a gyűrűben;
b) egy félkörben.

Legyen - területek kecske kivételével kutyák - a rendelkezésre álló területet a kutyák. Aztán figyelmét, hogy a kecske nem tudott kijutni a beállított különbség A \ B (definíció szerint egy pont tartozik az A \ B akkor és csak akkor tartozik egy, de nem tartozik a B, hogy pontosan ugyanazt a meghatározást kutya lépéseket a kecske).

a) az A gyűrű jelentése különbség a két kör van ugyanabban a központban. Ezért szükséges, hogy kössön egy kecske, hogy belépett egy nagy kört, és a kutya is - kevesebb.

b) félkör is képviselteti magát a különbség egy kör és egy téglalap vagy kör, és kitalálni a probléma 5. Lehet, hogy megoldja ezt a problémát egyébként, hagyja, hogy a kutya átnyúlnak a kör átmérője, a kötelet, és ezzel elosztjuk a kör két különböző részre. Akkor a kecske nem lesz képes mozgatni egy másik része a kör, és továbbra is egy félkör, ahol eredetileg volt. (Mellesleg, ez a példa azt mutatja, hogy a kecske nem feltétlenül megy át a beállított különbség, amely ebben az esetben jelenti az egész tartományban anélkül, hogy a szegmenst, mivel ez van osztva több független részből áll.)