Jegyek az első félévben - 6
keresztirányú törzs. Hozd megfelelő matematikai kifejezések,
bővíteni a fizikai tartozás érzését az értéküket. Adja meg a mértékegységet.
2. Hagyja meghatározása: a) egy normális stressz, b) az érintő (érintő) feszültségek. Adj egy megfelelő matematikai kifejezés, bővíteni a fizikai értelemben való tartozás az értéküket. Adja meg a mértékegységet.
3. Hagyja meghatározása: a) elasztikus kompressziós deformáció jog-nyújtás, b) a rugalmas nyírási deformáció törvény. Adj egy megfelelő matematikai kifejezés, bővíteni a fizikai értelemben való tartozás az értéküket.
4. Határozza meg a rugalmassági modulusa E az anyag. Nagyítás fizikai értelemben, adja meg a mértékegységet.
5. Sorolja fel a főbb típusai deformációk. Mi a legegyszerűbb típusú őket is csökkenthető.
6. Mi a különbség a rugalmas deformáció a műanyag?
7. Mi a különlegessége gumiszerű deformáció? Mi szervek jelen van?
8. Határozza meg a pillanat erő. Hozd megfelelő matematikai kifejezés, bővíteni a fizikai tartozás érzését értéküknek válasszuk egység.
9. Record alapfeltétele egyensúlya egy testet, amelynek forgástengelye.
10. Határozza meg a Poisson-tényező. hogy megfelelő
matematikai kifejezés, bővíteni a fizikai jelentését alkotó egységek.
Adja meg a mértékegységet.
11. megadják az anyag szilárdsága. Vedd alapvető feltétele a biztonság.
12. Mi az oka a különbség a technikai és elméleti erő? Melyik
őket leginkább és miért?
13. A főbb típusai a törés anyagok. Miben különböznek?
14. Fogalmazza a „hatalom szempontjából,” a feltétele mikrorepedéseken csírázást.
Magyarázatok köze a megfelelő ütemezést.
15. Melyek a fő mechanikai anyagvizsgáló lehet meghatározni
16. Definiálja a keménység az anyag. Sorolja az alapvető módszereit
meghatározását, így a megfelelő matematikai kifejezés, bővíteni
A fizikai tartozás érzését az értéküket. Adja meg a mértékegységet.
17. A csatlakozó fő mechanikai jellemzőit az anyag: a modul
Jung nyírási modulus és Poisson. hogy megfelelő
matematikai kifejezés, bővíteni a fizikai jelentését alkotó egységek.
18. Mi a neve a tartósságot az anyag, mi mérhető? ez attól függ,
tartósság az anyag az alkalmazott stressz? hoz
a megfelelő matematikai kifejezést, bontsa ki a fizikai értelemben tartozó
19. Hogyan működik a tartósság az anyag a hőmérséklet? hogy megfelelő
matematikai kifejezés, bővíteni a fizikai jelentését alkotó egységek.
20. Milyen fizikai értelmében „törékenység hőmérséklet TXP”
21. Minta „ORTOS - M” - alapanyagként szilikon párna kezdeti hossza 10 mm vetjük alá relatív húzóierheiésse 1,5. Határozza meg a kapott, amelynél a hosszúság és a minta.
22. Minta „ORTOS - M” - alapanyagként szilikon párna kezdeti hossza 20 mm nyújtásnak vetjük alá, hogy egy 30 mm hosszúságú. Értékének meghatározásához a relatív alakváltozás a minta.
23. Minta „ORTOS - M” - alapanyagként szilikon párna alá relatív húzóierheiésse 1,5, ahol a kapott minta hossza pedig 50 mm. Határozza meg a kezdeti a minta hosszának.
26. Mi a Young-modulusa a fog dentin, ha feszültség 250 MPa, a relatív mennyisége alakváltozás 1,5% volt
27. A termelő huzaleiemekre alkalmazott fogpótlás
rozsdamentes acél huzal. Vágott vezeték hossza L = 100 mm
Ez egy merevsége k = 5 mN / m. hosszának meghatározására huzal merevség 1,5-szerese
nagyobb keresztmetszetű 75 mm hosszúságú.
28. A gyártás a huzal elemek használt fogpótlás
rozsdamentes acél huzal. Vágott drót hosszúsága L = 90mm
Ez egy merevsége k = 3 MN / m. Határozza vezetékhossz merevség 1,5-szer kisebb a keresztmetszete, 75 mm hosszúságú.
29. A gyártás a huzal elemek fogpótlás használt rozsdamentes acélhuzal. Vágott vezeték hossza L = 100 mm merevsége k = 6 MN / m. meghatározzák a merevsége darab vezeték hossza 50 mm az azonos keresztmetszetű.
30. A gyártás a huzal elemek fogpótlás használt rozsdamentes acélhuzal. Vágott vezeték hossza L = 100 mm merevsége k = 8 MN / m. Határozza meg a merevsége a vezeték hossza a szegmens
200mm az azonos keresztmetszetű.
31. A gyártás a huzal elemek fogpótlás használt rozsdamentes acélhuzal. Vágott vezeték hossza L = 100 mm merevsége K = 9 MN / m. hosszának meghatározására huzal merevség 1,5-szer nagyobb keresztmetszetű és 1,5-szerese a hossza.
32. Mi lesz a merevsége a két párhuzamosan kapcsolt szakaszok ötvözet huzal, kapcsok gyártásához használt protézisek? Mindkét szegmense azonos hosszúságú huzal, de különböző keresztmetszetű. A keresztmetszete az első szakasz kétszer nagyobb, mint az utóbbi. A merevsége az első a szegmensek K1 = 4 MN / m.?
33. Mi lesz a merevsége a két sorba kapcsolt szegmensek az ötvözet huzal készítéséhez használt zárószerkezet fogsor? Mindkét szegmense ugyanazon vezeték-keresztmetszet, de különböző hosszúságú. A hossza az első szegmens kétszer. mint a második. A merevsége az első szegmens K1 = 5 mN / m.?
34. Hengeres minta kezdeti hossza 10 mm, készült ötvözet arany 900. mintát téve húzási vizsgálatok. Így a hossza növekedett 10,8 mm, és az átmérője csökkent 7 mm 6,8 mm. Határozzuk ötvözet Poisson.
35. Terhelés alatt, a mintát kibővítették a hosszanti irányban 2-szer, és a keresztirányban deformálódik 1.5. Határozzuk meg a Poisson-tényező az anyag.
36. Hányszor kiterjesztették minta hosszirányban, ha ez egy kereszt-deformált 1,3-szerese. Poisson-arány 0,25.
37. Hányszor deformálja a minta keresztirányban, amikor a hosszirányú
Ezt kiterjesztették 1,8-szerese? Poisson-arány 0,25.
38. befolyása alatt mechanikai feszültség 120 MPa, a mintát az elasztomer
Ezt kiterjesztették háromszor. Mi a nyírási modulus ezt az anyagot?
39. Hányszor kiterjesztették mintát elasztomer, amikor mechanikai
180 MPa feszültség, amikor a nyírási modulus ez az anyag 30 MPa.
40. Határozza meg a nyírási modulus az acél, ha a Young-modulus mert 200 GPa, és
Poisson-tényezője 0,3.
41. Határozza meg a rugalmassági modulusa E acél, ha a nyírási modulus érte egyenlő G = 80 GPa, és
Poisson arány 0,25.
42.Na ábra vázlatosan két híd támogatja a kétoldalú természetes fogak és B. Koncentrált F erő egyenlő 900 N alkalmazzuk a C pontban Határozza felfekvő reakció erő, és ha a = 4 cm, b = 2 cm
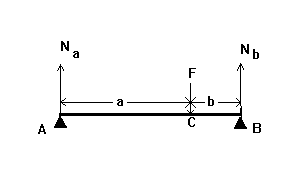
43.Na ábra vázlatosan két híd támogatja a kétoldalú természetes fogak és B. Koncentrált F erő egyenlő 720 N alkalmazzuk a C pontban Határozzuk meg a reakció erő a felfekvő ha a = 4 cm, b = 2 cm

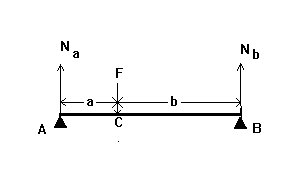
44. Az ábra sematikusan mutatja híd két bilaterális lábak természetes fogak és B Koncentrált F erő egyenlő 780 N alkalmazzuk a C pontban Határozzuk meg a keresztirányú erő Q keresztmetszete a X koordináta = 3 cm-re az A pont, ha a = 4 cm, b = 2 cm

45. Az ábra sematikusan mutatja híd két bilaterális hordozók
a természetes fogak és B Koncentrált F erő egyenlő 960 N alkalmazzuk a C pontban
Határozzuk meg a keresztirányú erő Q keresztmetszetben a koordináta x = 5 cm, attól a ponttól mérik
Egy, ha a = 4 cm, b = 2 cm

46. Az ábra sematikusan mutatja híd két bilaterális lábak természetes fogak és B Koncentrált F erő egyenlő 700 N alkalmazzuk a C pontban Határozzuk meg a hajlítónyomaték M (x) a szakasz koordinátái x = 6 cm-re az A pont ha a = 4 cm, és b = 3 cm.

47. Az ábra sematikusan mutatja híd két bilaterális lábak természetes fogak és B Koncentrált F erő egyenlő 840 N alkalmazzuk a C pontban Határozzuk meg a hajlítónyomaték M (x) a szakasz a koordináta X = 3 cm-re az A pont ha a = 4 cm, és b = 3 cm.

48. Az ábra sematikusan mutatja híd két bilaterális lábak természetes fogak és B Koncentrált F erő egyenlő 700 N alkalmazzuk a C pontban határozza meg a távolságot a referencia fogat egy, amelyben a hajlítónyomaték veszi a maximális értékét, ha a = 4 cm és b = 3 cm.

49. Az ábra sematikusan mutatja híd két bilaterális lábak természetes fogak és B Koncentrált F erő, amely egyenlő a 450 N, alkalmazzuk a C pontban határozza meg a távolságot a referencia fogat egy, amelyben a hajlítónyomaték van beállítva, hogy M = 2,1 N. m., ha a = 1 cm, és a
50. Az ábrán parcellák a potenciális energia W [J]
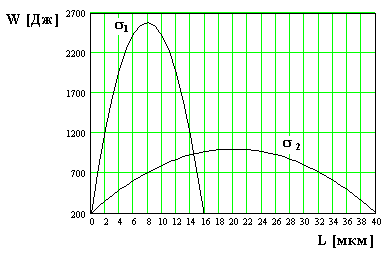
fosforokeramicheskogo minta anyag gyártásához felhasznált, a mesterséges
fogak a repedés hossza a két feszültség: 0,2 MPa és 0,6 MPa.
Határozzuk meg a legkisebb a repedés hossza, amelyből növekedni fog.
A mintát egy feszültség 0,6 MPa.
51. Az ábrán parcellák a potenciális energia W [J]
fosforokeramicheskogo minta anyag készítéséhez használt műfogak, a repedés hossza a két feszültség: 0,2 MPa és 0,6 MPa.

Határozzuk meg a legkisebb a repedés hossza, amelyből növekedni fog.
A mintát egy feszültség 0,2 MPa.
52. Az ábrán parcellák a potenciális energia W [J]
fosforokeramicheskogo minta anyag készítéséhez használt műfogak, a repedés hossza a két feszültség: 0,2 MPa és 0,6 MPa.

Határozzuk meg a maximális hossza a repedés. ahonnan nem fog növekedni.
A mintát egy feszültség 0,2 MPa.
53. Az ábrán a függőség a logaritmusa feszültség tartósságát az anyag
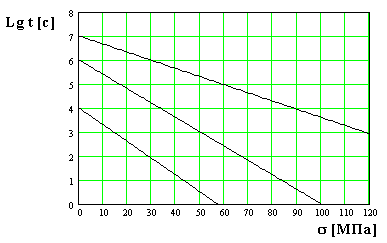
különböző hőmérsékleteken: 350 K, 300 K, 250 K
Határozza meg a tartósság az anyag hőmérsékleten 250 K és 90 MPa mechanikai igénybevétel.
54. Az ábrán a függőség a logaritmusa feszültség tartósságát az anyag
különböző hőmérsékleteken: 350 K, 300 K, 250 K

Határozzuk meg a tartósság az anyag 350 K és 30 MPa mechanikai igénybevétel
55. Az ábrán a függőség a logaritmusa feszültség tartósságát az anyag
különböző hőmérsékleteken: 350 K, 300 K, 250 K

Határozza meg a tartóssága az anyag hőmérséklete 300 K és 50 MPa stressz.
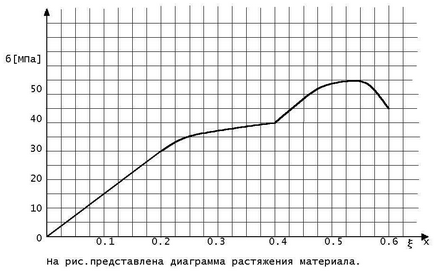
Hányszor rugalmassági modulusa nagyobb a szakítószilárdsága.

Hányszor feszített mintát a szakadás.
