Ball írt kúp
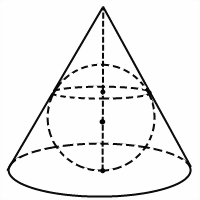
A kúp elfér bármilyen labdát. Feltüntetik egy labdát kúp (vagy gömb helyezhető be egy kúp) a kúp érinti a talajt a közepén, és az oldalsó felület - a kerület mentén. Központja a labda (gömb) fekszik a tengelye a kúp.
A problémák megoldása a labdát feltüntetik egy kúp, ez a legkényelmesebb, hogy fontolja meg a kombinált karosszériarészben áthaladó sík tengelye a kúp és a központ a labdát.
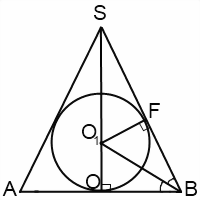
Az ezt a mintát képező SA = SB = l, a kúp magassága SO = H, a sugara a beírt gömb OO1 = O1F = R. Mivel a központ a beírt kör - a metszéspontja a szögfelezői a háromszög, majd ∠OBO1 = ∠FBO1, OB = r - a sugara a kúp.
Vegyünk egy derékszögű háromszög zokogását. Az ingatlan a felezővonal a háromszög:
A tétel Pitagorasz
Vegyünk egy derékszögű háromszög OO1B.
Ha ∠OBS = α, majd ∠OBO1 = α / 2. itt
Ha első kifejezni a sugara a kúp révén a magassága egy derékszögű háromszög SOB
háromszögének OO1B kifejezetten a sugara a labdát át a kúp magassága: