A módszer a Fresnel zónák
Fresnel javasolt egy eredeti módszer bomlása a hullám S felület az övezetben, ami lehetővé tette nagy mértékben egyszerűsíti a problémák megoldását (eljárás Fresnel zónák).
A határ az első (középső) terület S. felületi pont olyan távolságban az M pont (ábra. 9.2). S. pont a gömb a távolból. . stb attól a ponttól, M. alkotnak 2, 3, stb Fresnel zónában.
A gerjesztett rezgések az M pont közötti két szomszédos zónák ellentétes fázisú, mivel a pálya különbség ezekben a zónákban, hogy a pont M.
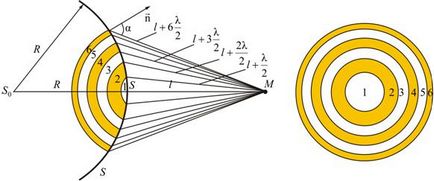
Ezért, ha hozzá ezeket a rezgéseket, az általuk kölcsönösen gyengíthetik egymást:
,
ahol A - amplitúdója a kapott oszcilláció, - az amplitúdó a gerjesztett rezgések által az i-edik Fresnel zónában.
Az érték függ a téren zónák és az a szög között normális vonal a felszínre, és egy olyan hely felé M.
A terület egyik zóna
.
Ez azt mutatja, hogy a terület a Fresnel zóna független az i számú zónában. Ez azt jelenti, hogy ha nem túl nagy i területen a szomszédos zónák azonos.
Ugyanakkor a növekedés a szög zóna szám növekszik, és így, az intenzitás a sugárzási területen csökken afelé a pont felé M. azaz csökkent amplitúdó. Ugyancsak csökkenti a növekvő távolság az M pont:
.
A teljes száma Fresnel zónák elfér gömbrész felé eső ponton M. nagyon nagy: a. . a zónák számát. és a sugara az első zóna.
Ebből következik, hogy a szögek között normális, hogy a területet és az irányt, hogy pont M szomszédos zónák közelítőleg egyenlő, azaz hogy az amplitúdó a hullámok érkező tochkuM a szomszédos zónák nagyjából megegyezik.
A fény hullám szaporítjuk egy egyenes vonal. Lengések izgatott a szomszédos zónák különböznek π. Ezért, mint egy érvényes közelítés lehet kiindulni, hogy az oszcilláció amplitúdója a m-edik zóna a számtani átlaga amplitúdóinak szomszédos zónák, azaz a
.
Ezután a kifejezést (9.2.1) felírható
.