A maximális térerősség a távolság függvényében

Nézzük megoldani a több összefüggő problémák meghatározása a térerősség különböző távolságokban a tárgy, amelynek a forrása a területen. Ott kell emlékezni a szabályokat figyelembe a származtatott egy összetett függvény, valamint a határ függvénye.

Probléma 1. Amikor az elektromos térerősség V / m levegő már nem megbízható és a szigetelő a szikra kisülés lép fel abban. Mi legyen a sugara a fém gömb, hogy tartható a 1 C töltés?

A térerősség által adott töltésű gömb

Ezért tapasztaljuk, hogy a tartomány:

Probléma 2. A csúcsai egy tér oldalán elhelyezett négy azonos töltés. Határozzuk meg a maximális térerősség az átmenő tengely a közepén egy négyzet a síkjára merőleges. Milyen messze van a téren a legnagyobb?

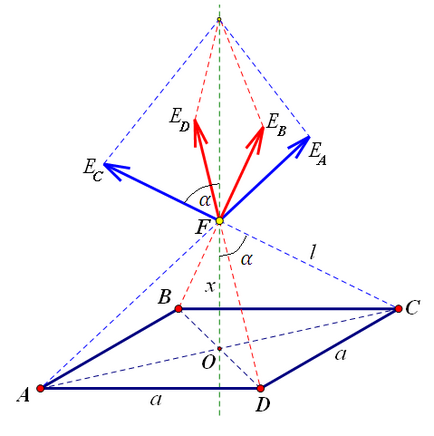
Mind a díjak hogy hozzájárul a teljes térerő egy adott ponton. Feszültség vektorok a pár díjak ellentétes sarkokban, részben kompenzálja egymást: a vízszintes elemek (vetülete egy négyzet sík) az összeg ad nulla. Ezért, a forma függőleges lesz komponenseket - a vetülete a feszültség a függőleges tengelyen. A vetítés a térerősség a függőleges tengelyen egy feltöltéssel egyenlő:

Négy díjat:

Távolság tölteni. Mi határozza meg. Ha az oldalán a tér. akkor az átló. és fél átlósan -. Hagyja, hogy a távolság négyzetével a sík a pontot. . majd

Ebben a képletben, - változó hosszúságú. Ahhoz, hogy megtalálja a legnagyobb a funkciót. hogy a származék:

Mi egyenlőségjelet tesznek a származékos nullára, hogy megtalálják a szélsőérték:

Azt állapítottuk meg azt a távolságot, amely az intenzitás maximális - látható az a tény, hogy ez a csúcspontja, hogy meghatározza a jel a származékos a bal és a jobb a pont. Most tudjuk helyettesíteni a képletbe az a távolság, a területen, és meghatározzák azt a maximális intenzitása:

Válasz: A maximális intenzitás érhető el bizonyos távolságra a sík a téren.

Probléma 3. A vékony huzal gyűrű egy sugara töltés. Keresse térerősség az a gyűrű tengelye olyan távolságban közepén. Ábrázoltuk.

A feladat hasonló az előzőhöz. Csak most elemi díjakat osztott egy gyűrű, és minden díj létrehoz egy vektor a feszültséget. Így megkapjuk a felületre, mint egy kúp, amely a feszültség vektor egyes elemi díjakat.

Ha állsz a közepén a gyűrűt, majd a vektort teljesen kompenzálják egymást, és a teljes ereje nulla lesz. Azonban, ha azt váltás egy kicsit jobbra vagy balra ezen a ponton, a feszültség nem lesz nulla, mivel ezek a vektorok a longitudinális komponens lesz, és ez az összeg az összes ezeket a komponenseket, és megadja a térerősség bármely pontján a tengelye a gyűrű, távol a távolságot. Elemi töltés egyaránt megtalálhatók. A feszültség az általuk létrehozott,

Ahol. és a koszinusz a szög

Mező erőssége az összes díjak:

Ahhoz, hogy megtalálja a legnagyobb a funkciót. hogy a származék:

Mi egyenlőségjelet tesznek a származékos nullára, hogy megtalálják a szélsőérték:

Határozzuk meg a maximális térerősség ezen a ponton, hogy ebben az esetben a távolság a kifejezést a feszültséget:

Azt találtuk, hogy a központ a gyűrű térerősség nulla, és nő a távolság. amíg el nem éri a maximális távolból. Most nézzük meg, mi lesz egyenlő a feszültség végtelen távolság: tart végtelenbe.

Mivel ez a funkció mind a számláló és a nevező, és mi van a fajta bizonytalanság végtelenig a végtelenbe, akkor határozza meg a határt L'Hospital-szabály:

Tehát, meg lehet építeni egy grafikon:

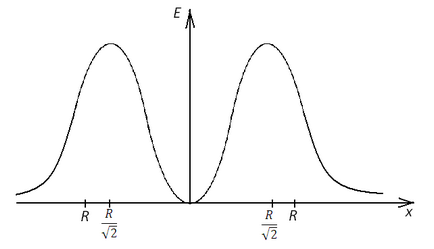
Probléma 3, a grafikon