A középső sorban a trapéz
Megmutatjuk, hogy $ MN || AD \ és \ MN = \ frac $.
Tekintsük a vektor $ \ overrightarrow $. Mi használ általában sokszög vektor kívül. Egyrészt, azt találjuk, hogy
Másrészt
Elhelyezés az utolsó két egyenletet, megkapjuk
Mivel $ M $ és $ N $ - a középső oldalán a trapéz, akkor van
Ugyanebből a egyenlőség (mivel a $ \ overrightarrow $ és $ \ $ overrightarrow ugyanabba az irányba, és így egy egyenesre), hogy a $ MN || AD $.
Példák célok a koncepció középvonal trapéz
Az oldalán a trapéz $ 15 \ cm $ és $ 17 \ $ cm volt. Kerülete trapéz egyenlő 52 $ \ $ cm. Keresse meg a hossza a középvonal a trapéz.
Jelöljük a középvonal a trapéz a $ n $.
Az összeg az oldalak egyenlő
\ [15 \ cm + 17 \ 32 cm = \ cm \]
Következésképpen, mivel a kerülete egyenlő $ 52 \ $ cm, a bázis mennyisége
\ [52 \ 32-cm \ cm = 20 \ cm \]
Ezért, 1. tétel, megkapjuk
A végén a kör átmérője, kiveszik a tangens rendre $ $ 9 cm, és $ 5 $ cm. Keresse meg a kör átmérője.
Tegyük fel, hogy adott egy kör középpontja O $ $ és $ átmérője AB $. Felhívjuk egy érintő $ l $ és a kivitelezést távolságban $ AD = 9 \ cm $, és $ BC = 5 \ $ cm. Döntetlen sugara $ OH $ (ábra. 2).
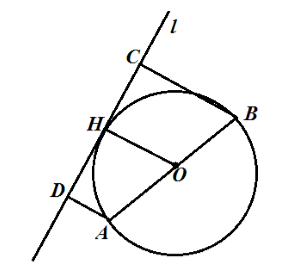
Mivel $ AD $ és $ BC $ - távolság a tangens, a $ AD \ bot l $, és $ BC \ bot l $, és mivel $ OH $ - sugara, a $ OH \ bot l $, ezért, $ OH | \ left | AD \ right || BC $. Mindezekből azt látjuk, hogy a $ ABCD $ - trapéz és $ OH $ - a középső sorban. By 1. tétel, megkapjuk
\ [D = 2OH = 2 \ cdot 7 \ cm = 14 \ cm. \]