Algorithmization és alkalmazás programozási (d negodin
akkor T (n) = N ln N. minden N = 2 k. k> 1.
2. Keresés egy adott elem lineáris keresési módszer (2 benyújtása válogatás algoritmus betétek) összehasonlítjuk az elemek elejétől a tömb. A rendezett tömböt használhat, ha összehasonlítjuk a kívánt pontra az elrendezés közepén, majd válassza ki a részét, amelyben található, és ismételje meg ezt a részét rekurzív osztály, és így tovább - a bináris
ny keresést. Írj programot, amely végrehajtja az algoritmus, és bizonyítani, hogy működése vannak Θ (ln N).
3. míg Ciklus Insertion_Sort eljárással megvizsgálja az összes elemet a leválogatott sor részét. Ehelyett, akkor a bináris módszer
Keresés (2. gyakorlat merge sort algoritmus), hogy megtalálja a kurzort idő Θ (ln N). Írja a megfelelő végrehajtási eljárások
Insertion_Sort és meghatározza, hogy az ilyen módon képes arra, hogy egy teljes időt egyenlő Θ (N ln N).
egyesítése rendezési algoritmus
4. Legyen betétek válogatás és összevonása végezzük ugyanazon a gépen, és szükség 8 N 2 és N ln N 64 műveletek, ill. Mert mi N értékek behelyezés fajta hatékonyabb? Hogyan növelhetem egyesíteni rendezési algoritmus?
5. Amikor a legkisebb értéket N, amely algoritmust 100 igényel N 2 műveletek, hatékonyabb algoritmust igényel N 2 műveleteket.
1. merge sort aszimptotikusan gyorsabb válogatás betétek, de az N fordított viszonyban van a kis értékeket. Ezért van értelme meglehetősen rövid darab nem osztódnak tovább, és rendezni betétekkel.
1.1. Legyen egy sor méretű N osztva k alkatrészek, k N mérete. Mutassuk meg, hogy
az összes rész lehet válogatni külön (a betétek válogatás) során Θ (kN).
1.2. Mutassuk meg, hogy le lehet engedni a válogatás után a darabokat egy rendezett tömbben időben Θ (N ln (N k)).
1.3. Átlagos ideje E vegyes algoritmus Θ (nk + N ln (N k)). Mi a legnagyobb növekedési üteme k függvényében
N., amelyben ez az idő még mindig egyenlő Θ (N ln N)?
1.4. Hogyan állapítható meg az optimális k érték a gyakorlatban.
2. Legyen adott tömb egy [1 N]. Inverzió a tömb egy pár egészek i
2.1. A maximális számát inverzió a tömb hossza N.
2.2. Hogyan lehet kapcsolatba lépni a futási ideje válogatás lapkák és a fordítások számát? Indokolja válaszát.
2.3. Construct algoritmus, amely megszámlálja az inverzió a tömb hossza N egy időben Θ (N ln N).
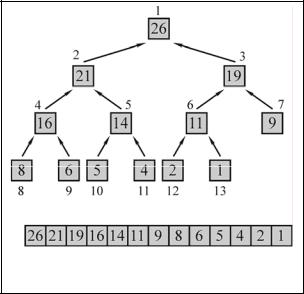
3. ábra - Példa a bináris kupac
A rendezési algoritmus alkalmazásával halom (Heap)
A rendezési algoritmus alkalmazásával halom (Heap)
Szortírozás alkalmazásával kupac igényel annak üzemidő T (n) = Θ (N ln N). de ellentétben az egyesítési algoritmus nem igényel ilyen nagy
további memóriát változókat. Azaz, az algoritmus egyesíti a rendezési algoritmusok, behelyezés (használjon egy további kis mennyiségű memória), és a fúziós eljárás (rövid idejű munkavégzés).
Az adatszerkezet, amely egy algoritmus az úgynevezett bináris kupac, célszerű, ha a prioritásos sor.
Bináris kupac nevezzük egy tömb bizonyos tulajdonságait rendelés. Megfogalmazni a tulajdonságokat vesszük tömb, mint a bináris fa. Minden egyes csomópont a fa felel meg egy elem - 3. ábra.
Ha a csomópont egy olyan i index. hogy a szülő rendelkezik indexszel int (I / 2). és PO-
Tomka 2 i 2, és i + 1 A csúcsból index i = 1 egy gyökér. A memóriában tárolt tömb. hossza N és egy speciális paraméter Heap _ méret - a méret a kupac, és
Heap _ Méret ≤ N. Egy rakás elemekből áll egy [1] ... egy [Heap _ Size]. Navigálni a kupac által használt három funkciót:
A tárolt elemekkel a halom, a halom kell rendelkezniük alapvető tulajdonság: az összes elem, kivéve a gyökér, meg kell felelnie a feltételt egy (I) szülő ≥ a [i],
azaz az érték az utód nem lehet több, mint egy ős, ami azt jelenti, hogy a gyökér a fa a maximális elemet.
Magassága a fa tetején az úgynevezett magassága részfa gyökere ennek a csúcspont (az élek száma a leghosszabb út kezdődik a tetején ez a fát). Fa magassága egybeesik a magassága a gyökér.
A fa alkotó egy kupacban, minden szinten, kivéve talán az utolsó, teljesen kitöltve, így a fa magasságát is Θ (ln N). ahol N - száma
elemeket a kupac.
Tekintsük az alapvető eljárásokat dolgoznak egy csomó:
1. Heapify - támogatja az alapvető kupac tulajdonság, a teljesítménye azonos
A rendezési algoritmus alkalmazásával halom (Heap)
2. Build_Heap - épít egy csomó eredeti szelektálatlan tömb, a teljesítmény egyenlő Θ (N).
3. Heap_Sort - válogatás nélkül további memória, az átfutási idő Θ (N ln N).
4. Extract_Max (eltávolítása a legnagyobb) és betét (betét) létrehozásához használt prioritási sor alapján a kupac. Munkaidő mindkét eljárások Θ (ln N).
Preservation tulajdonságok fő halom
Heapify eljárás paraméterek (a, i) egy tömb és az index a i. Feltételezzük, hogy a részfa gyökerezik Bal (i) és a jobb (i) már alapvető tulajdonságait. Eljárás átrendezi részfa csúcsú i. majd ez lesz az alap tulajdonságait. Az ötlet egyszerű: ha az alap tulajdonság nem valósítható meg a felső, akkor meg kell változtatni egy csomó a gyerekek, és így tovább, amíg a tételt nem „mosogató”, hogy a megfelelő helyre.
Tekintsük Heapify eljárás (A, I)
3, ha (L≤Heap_Size) és (a [L]> a [i])
4, majd Legnagyobb: = L
5 mást Legnagyobb: = R
6 Ha (R≤Heap_Size) és (a [R]> a [legnagyobb])
7, majd Legnagyobb: = R
9 majd a swap (a [i], a [legnagyobb])
A változó index legnagyobb elhelyezett legtöbb elemét a [i],
Bal (i) és a jobb (i). Ha a végén Legnagyobb = i ciklus. Az a [i] elemnek
„Zuhant”, hogy a megfelelő helyen és a munka befejeződött az eljárás. Ellenkező esetben, az eljárás megfordítja egy [I] és [Legnagyobb]. de lehet, hogy sérti a
Fő tulajdonságok részfa a tetején legnagyobb és visszatérően hivatkozott Heapify eljárást megszüntesse az esetleges megsértése.
Átfutási idő a legrosszabb esetben ennek az eljárásnak, a T (N) = Θ (ln N).
Tegyük fel, hogy kapnak egy tömböt egy [1 N]. ami kell alakítani egy halom. Ehhez, akkor lehet alkalmazni Heapify eljárást. alkalmazva azt a fordulatot, hogy a magasban, kezdve az alján. A csúcsok számozott [N 2] + 1 ... N a levelek, majd
részfák azokkal levelek már megfelel az alapvető tulajdonság a halom. Az egyes megmaradt csúcsok csökkenő sorrendben az indexek kell alkalmazni pro-
2 az I: = int (N / 2) downto 1 do
A maximális idő az eljárás T (N) = Θ (N).
Küld a kupac
rendezési algoritmus két részből áll, az első okozza Build_Heap eljárást. konvertáló a tömb egy halom.
A második rész közvetlenül szabályozza a halom. Legnagyobb halom elem a gyökér a fa - az elem a [1]. Ez az elem cserélték
elem egy [N]. kupac mérete csökken 1-gyel és helyreállítja az alapvető tulajdonsága a halom, hogy a gyökér csúcs (mint a részfa gyökerezik bal (1) és a jobb (1) Az alapvető tulajdonsága a halom nem megszakítható) az Heapify eljárást.
Ezt követően, a gyökér lesz a legnagyobb a többi elem. Ezután, az átrendeződés egy [1], és egy [N - 1]. Ismét, az eljárást végzik
Átrendezése elemek addig folytatódik, amíg, amíg a teljes tömb rendezve.
2 az I: = N downto 2 do
eljárások az idő T (n) = Θ (N ln N).
A gyakorlatban a rendezési algoritmusok nem használja kupac leggyorsabb, de maga a szerkezet csomó frekvencia adatok hasznos.
prioritásos sor
Prioritású sorba (prioritási sor) - egy sor olyan elemeket, amelyek figyelembe kell venni számokat. A gyakorlatban, az elemek S párok
Chom, α - kapcsolódó tudnivalókat ezt az információt tárolja mellett, és mozog vele, anélkül, hogy annak kezelése. Az egyszerűség kedvéért kihagyja a leírás a műveletet a további adatokat.
A következő műveleteket a sorban prioritások:
1. Insert (S, x) hozzáad egy elemet x a beállított S;
2. Maximum (S) visszaadja a legnagyobb eleme a készlet;
3. Extract_Max (S) eltávolítja a legnagyobb eleme a készlet;
4. Extract_Min (S) eltávolítja azt a legkisebb elemet a több.
Prioritási sort is, például lehet használni az operációs rendszer időosztásos. Ugyanakkor ez tartja a feladatok listáját a prioritás
A rendezési algoritmus alkalmazásával halom (Heap)
tetami. Amint a végrehajtás a következő feladat befejeződik, a feladatsor van kiválasztva a legmagasabb prioritású (Extract_Max művelet). Új munkahelyek adunk a sorból, a Beszúrás működését.
Egy másik alkalmazás az azonos szerkezetű - eseményvezérelt szimuláció (esemény szimuláció). A sorban vannak események, és a prioritás határozza meg, amikor az esemény következik be. Események kell modellezni, abban a sorrendben, amelyben előfordulnak. Kiválasztása a következő esemény végezzük Extract_Min működését. események hozzáadását - révén működés
Tároltuk az elemek egy halom. A maximum a gyökér elem, hogy a művelet időt vesz igénybe Maximum Θ (1).
Ahhoz, hogy távolítsa el a legmagasabb elem a sorból, meg kell cselekedni, valamint a válogatás: