Lebonyolítása a közös érintő a grafikonok két kvadratikus függvények
Class 10 "D", belorusz National Technical University Líceum, a Belarusz Köztársaság, Minszk
Lyakh Alla Saturinovna
Kutatási vezetője, oktató a matematika, a Nemzeti Műszaki Egyetem Líceum, a Belarusz Köztársaság, Minszk
Ezekben a kvadratikus függvények vezető együtthatók 1 és -1, azaz. E. Mindkét parabola ága, különböző irányba mutató. Ahhoz, hogy meghatározzuk a metszéspontjait a grafikonok egyenlővé jobb oldalán egyenleteket (⃰⃰) és
megvizsgálja grafikonok előre meghatározott helyzeti viszonyt görbék különböző értékei az együtthatók és.
1) Ha. a parabola két közös pont.
2) Ha. a parabola egy közös pont (érintsék egymást).
3) Ha. A parabola nincs közös pont.
Most tartsa a közös érintők, hogy a parabola:
Hagyja közös érintője érinti a parabola a ponton. parabola - egy pont (1. ábra)
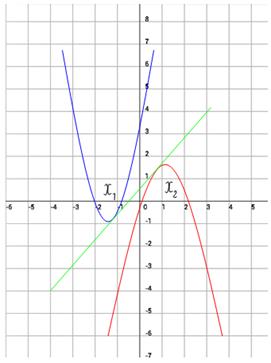
Írunk egyenlete érintő a görbe:
Írunk egyenlete érintő a görbe:
Az az állapot, teljes egybeesése két érintő egyenlő megfelelő együtthatók:
Így van egy egyenletrendszert:
Ennek eredményeként az átalakulások kapjuk a következő egyenletet:
1) Ha. a parabola két közös pontja van, és ebben az esetben lehetetlen felhívni a közös érintője.
Következtetés: parabola, amelynek vezető együtthatók 1 és -1 (parabola közös két pont), nincs közös érintője.
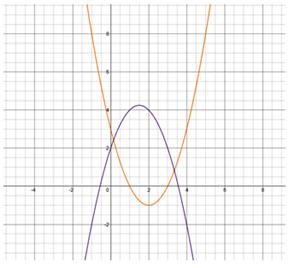
2) Ha. A parabola van egy közös pont (érintkeznek egymással), és ebben az esetben csak egy közös húzott érintő érintési pont parabola - érintési pont.
Közös érintője egyenlet a következő formában:
Következtetés: parabola, amelynek vezető együtthatók értéke 1 és -1. (Parabola lesz egy közös érintkezési pont), lehet végezni a közös érintőjének az érintési pont.
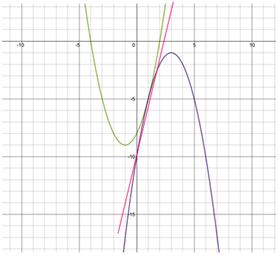
Az egyenlet az érintő és tapintási pont:
3) Ha. A parabola nincs közös pont, és ebben az esetben lehetséges, hogy két közös érintők.
Legyen A és C pontok érintési parabolákat grafikonok esetén egy, a B, és D - a másik.
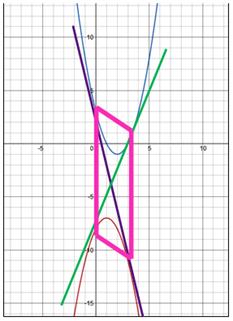
közös érintője egyenlet a következő formában:
Megjegyezzük, hogy a négy ponton érintkező két közös érintők alkotnak négyszög ABCD, amelynek oldalai AB és CD egyenesek párhuzamosak.
Mi bizonyítja, hogy a négyszög paralelogramma.
Mivel a pontok koordinátáinak az M1 és M2 meccs négyszög ABCD - paralelogramma.
Következtetés: parabola, amelynek vezető együtthatók 1 és -1, és a (parabola nem lesz közös pontja) elfér két közös érintők, és a fogási pont lesz a csúcsok egy paralelogramma, két oldala párhuzamos az Y-tengely.
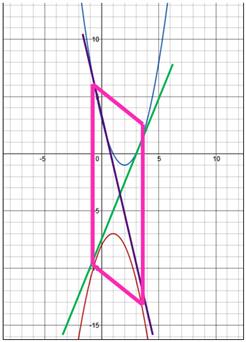
Az egyenletek érintők és pontok:
2.Entsiklopedichesky szótár fiatal matematikus. Comp. Savin, AP M. Pedagógia, 1985 - 352 p.;