A képletek és fogalmak, a rugóerő, az erő a gravitációs kölcsönhatás (törvénye
1. A súrlódási erő
ahol a súrlódási tényezőt; abszolút értéke a normális nyomóerő; egységvektor irányában a test sebessége.
ahol a merevség együtthatók;
- merevségi tényezője a sorozat kapcsolatot a rugó rugóállandója, illetőleg;
merevségi tényezője a párhuzamos kapcsolása rugók és a merevség együtthatók rendre; koordinálja a szabad végén a tavasz; ez ugyanaz a nem feszített rugó. A mínusz jel azt jelzi, hogy az erő van irányítva, ellentétes irányban a törzs.
ahol Nm / kg 2 - gravitációs állandó; ; rádiuszvektorhoz a 2 test a testsúlyhoz 1. A mínusz jel jelzi vonzás szervek.
ahol a gravitációs gyorsulás (a felület közelében); m / s 2;
ahol a tömeg és sugara a Föld (bolygók, csillagok), illetve; magasság fölött a Föld felszínén.
5. A szuperpozíció elve: Ha egy anyagi pont van több erő, minden egyes ilyen erők szerint az anyag gyorsulása szerint Newton második törvénye, mintha a többiek nem volt ereje. Ezen elv szerint, az erő és a gyorsulás bontható komponensek. A ható erő anyagi pont mentén mozgó görbe bontható két komponens - a tangenciális és normális.
Tangenciális (vagy érintőleges) erő
ahol az egység vektor irányított mentén érintő a pályához.
Normál (vagy centripetális) erő
ahol a görbületi sugár az útvonal; az egység vektor mentén merőleges a pályára.
1. A lendület anyagi pont
ahol - a sebesség az anyag pont.
2. Az impulzus a rendszer
ahol - tömeg edik részecske - a sebességét annak egy Inerciarendszer.
Newton második törvénye
ahol a geometriai összege ható erők anyagi pont; - az impulzus; - száma ható erők a lényeg.
2. Ha a tömeg állandó, Newton második törvénye a klasszikus mechanika fejezhető ki képlettel
3. Ha nem tudja a pontos jogszabály, amelynek értelmében a teljes erőt változások
a testre ható, akkor a koncepció átlagos erő bizonyos ideig mostantól egészen.
Ekkor az egyenlet Newton második törvénye felírható
ahol - a változás a lendület az azonos időszakra vonatkozik; nevezik a termék az átlagos impulzus teljesítmény.
4. Newton második törvénye a koordináta (skalár) formában
ahol az összegzés jele az előrejelzések az erők a megfelelő tengelyek.
Newton harmadik törvénye
ahol - a ható erő az i-edik anyagi pont a k-adik anyagi pont; - ható erő a k-adik anyagi pont az i-edik anyagi pont. Ható erők egymásra lényeges pontokon mindig egyenlő nagyságú alkalmazzák különböző pontjain az anyag ellentétesen vannak irányítva, mindig párban és cselekedni egy egyenes vonal mentén összekötő ezeket a pontokat.
2. Besorolás problémák és ajánlások, megoldási módszerek
Feladatok a dinamikáját lineáris mozgás egy anyagi pont alapján a módszer azok oldat, lehet osztani az alábbi fő típusai.
1) Az összes erők. a testre ható egybeesik a sorban, amely mentén a gyorsulásvektor irányul. Ebben az esetben az egyenlet Newton második törvénye formájában vektor és skalár oldat formában végzik, figyelembe véve az irányt az erők.
2) Ha az erő a testre ható különböző irányba (továbbá néhány közülük nem esnek egybe az irányt, mint a test mozgás egy ferde sík) .:
· Jelölje bármely két OX és OY tengelyek (, hogy egyszerűsítse a megoldások, kívánatos, hogy irányítsa az egyikük mentén gyorsulásvektor);
· A projekt összes ható erőket az OX és OY;
· Írja le Newton második törvénye, illetve az x-tengely:
· Problémák egyenletek együtt (ha szükséges egészíteni a megfelelő kinematikai egyenletek a mozgás).
3) mozgása több erő kapcsolódó súlytalan és nyújthatatlan anyagból (mozgása több szerv a vízszintes és a ferde síkok; feladatokat tömb, amely ível át egy szál - kötél, kötél, kábel, stb).
Alaptörvényei a problémák megoldását a blokkot lehet a következőkben foglalhatók össze:
· Súlytalan blokkok száma (vagy tömeges figyelmen kívül lehet hagyni);
· A téma szervek közötti tekinteni súlytalan és nem nyújtható;
· Fonal feszültsége erők mindkét oldalán ugyanazon egység;
· Newton második törvénye rögzíti minden szervezet külön-külön (a kiválasztott mozgási irányára rendszerének szervek);
· Ha a fonalat dobott, például, miután 2 súlytalan egység (a - a mozgatható második - álló), a szálfeszítő fogja kényszeríteni a teljes hossza azonos, ám a gyorsulás a mobil egység teherforgalom más.
3. Példák megoldása tipikus problémák
A ballon súly M250 kg kezdett esni a gyorsítás 0,2 m / s 2. Határozza meg a súlya a ballaszt, amelyet meg kell állítani, hogy a ballon megkaptam ugyanazt a gyorsulást, de felfelé. Nehézségi gyorsulás 9,8 m / sec 2 légellenállás elhanyagolható.
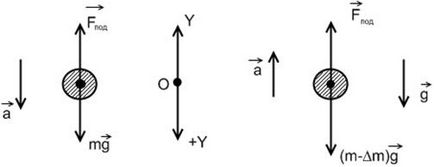
Megoldás: Mivel a ballon cseppek gyorsulás. kevesebb gravitációs gyorsulás. és azzal a feltétellel, a probléma nem a légellenállás, az azt jelenti, hogy úgy viselkedik, amellett, hogy az emelés a gravitációs erő. függőlegesen felfelé.
Reagálás a ballon erők függőlegesen, tehát az egyenlet a mozgás
elegendő ahhoz, hogy a projekt csak az egyik tengelyen OY koordinátarendszerben:
Ha a felvonó
Ha visszaállítja a nehezék. akkor az egyenlet a mozgás felírható
illetve az abból eredő kifejezés a felhajtóerő
Következésképpen, a tömege ballasztvízben van
Jármű, mozgó sor 5c egységesen fel kell gyorsítani a sebességet 72 km / h.
Keresse meg a lehető legkisebb súrlódási együtthatót a jármű kerekei és az út során ezt a mozgást.
Mi az a legkisebb féktávolság az autó, amely megkapta ezt a sebességet?
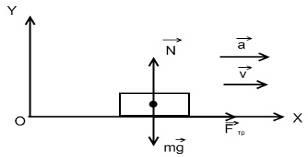
Megoldás: Ha a jármű mozgásban van, mind a gyorsulás és a fékezés, neki van három erő: a gravitáció. normál erő az útról súrlódási erő
a) A gyorsított a jármű mozgásának a súrlódási erő megakadályozza elcsúszását a meghajtó kerekek az útfelületre, így van irányítva, a mozgás irányát és erő statikus súrlódás. Ez az erő a tapadási súrlódás ebben az esetben lesz a hajtóerő. Ennek alapján a kiválasztott XOY koordinátarendszerben, az egyenlet a mozgás adja
Az előrejelzések a koordinátarendszerben tengely:
Kifejező súrlódási erő révén a reakció erő és a súrlódási együttható a kerekek és az út
Az egyenletek a mozgás határozza meg a jármű gyorsulását:
Másrészt, mert a probléma feltételek haladó autó egyenletes gyorsulás az idő felgyorsult. A gyorsulás
Véleménynyilvánítás van 0.41. ezért
b) Amikor a fékezési súrlódási erő ellentétes irányúak, hogy a mozgás és a csúszó súrlódási erő. Az egyenlet a jármű mozgásának ebben az esetben a nyúlványok a koordinátatengelyeken
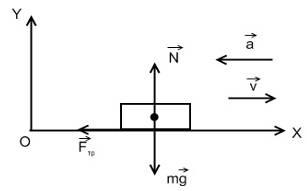
Tekintettel arra, hogy. gyorsítás során a jármű fékezés
A megtett út az autó mozog kezdeti sebességgel ravnozamedlenno jelentése
Az idő a mozgás leállításához lehet meghatározni a feltétellel, hogy az utolsó jármű sebessége
Mivel a kifejezés a súrlódási együttható (7), megkapjuk
Egy sima ferde sík szögben és az alaplapra van M tömegű és hirdetőtáblák - blokk tömege m. Fedélzeti ható erő fel a hegyre. Milyen értéken ennek az erőnek, a tömeg kezd csúszni? A súrlódási tényező a fedélzeten, és a bárban. Gravitációs gyorsulás.
Megoldás: A ható valamennyi szerv egy Inerciarendszer XOY látható Fig.2.4.
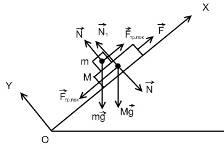
A bárban a gravitációs erő hat,. a súrlódási erő. erő és a reakció erő; fedélzetén a gravitációs erő hat,. reakció erő. a súrlódási erő és a tömeg a bárban egyenlő nagyságú. Figyelembe vesszük, hogy
Írunk a Newton második törvénye a kiemelkedések a tengely a kiválasztott koordináta-rendszer, feltéve, hogy a testület nem csúszik bar:
Megoldása az egyenletrendszert, megkapjuk.
Ezért, amikor a bárban csúszik le a tábláról.
Egy ferde síkon szögben tövében van fixen kocka. A súrlódási együttható közötti ék és a kocka egyenlő. Ferde sík mozog gyorsulás irányába ábrán látható. 2.5. Hogy milyen minimális értéke a gyorsulás a kocka elindul, hogy csúszik?
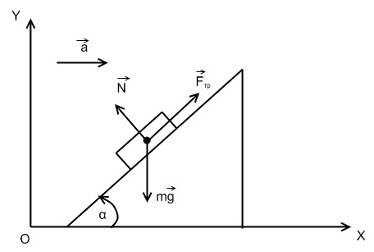
Megoldás: Írunk Newton második törvénye a előrejelzéseket az x-tengely OY és az inerciális vonatkoztatási rendszer, társítva a Föld, figyelembe véve, hogy egy kocka képest az ék nyugszik:
Mivel a kocka többi viszonyítva az ék, majd kapcsolódnak. azaz
Következésképpen, ha a kocka elkezd csúszni a gyorsítás során az ék egyenlő
Ha. a test kezd csúszni bármikor tetszőlegesen kis gyorsítást.