Vizsgálata stabilitásának lineáris automatikus ellenőrző rendszerek 1
Cím a munka: Kutatási stabilitásának lineáris automatikus ellenőrző rendszerek
Szakterület: Kommunikáció, kommunikációs, elektronikai és a digitális eszközök
Leírás: A ugrásválasz az automatikus vezérlő zárt állapotban egy grafikus formában a grafikonon a tranziens válasz a rendszer világosan látható, hogy a rendszer az adott paraméterek instabil. A frekvencia és a pulzus jellemzői a folyamat: a napló az amplitúdó-frekvencia és a fázis-frekvencia karakterisztika.
Fájl mérete: 860,5 KB
Job letöltve: 25 fő.
A laboratóriumi munka
Fegyelem: „irányító rendszerek kémiai technológiai folyamatok”
Cím: „Tanulmány a stabilitás lineáris automatikus ellenőrző rendszerek”
Használata szerkezeti modellezési módszer (összpontosítva használata a számítógépes rendszer MatLab matematikai vagy MathCAD) vizsgálja, előre meghatározott automatikus ellenőrző rendszer stabilitását. Annak megállapítására, befolyása rendszer paramétereit annak stabilitása és megtudhatjuk, hogy határ (kritikus) értéket.
Háttér (MODE 6):
Egy adott ACS hogy távolítsa el a menetrend átviteli függvény és annak szem előtt, hogy meghatározzuk a rendszer stabilitását.
A blokk diagram az automatikus vezérlés zárt állapotban.
Simulink-modell az ACS zárt helyzetben a «MATLAB»:
Tranziens válasz az ACS zárt helyzetben grafikus formában:
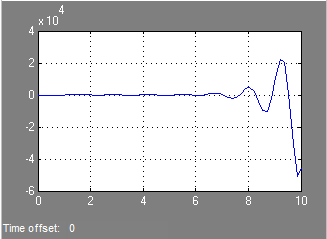
átmenetet rendszer jellemzőinek egyértelműen látható a grafikonon, hogy a rendszer instabil alatt adott paraméterek.
Frekvencia és pulzus jellemzői a folyamat:
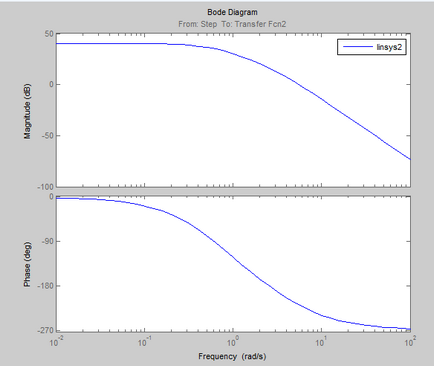
Logaritmikus amplitúdó-frekvencia és fázis válasz (Bode diagram)
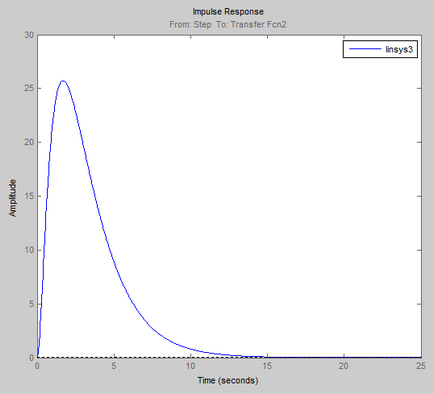
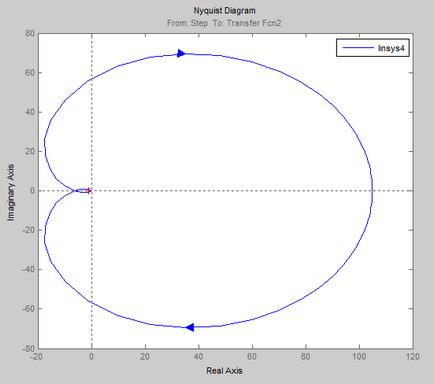
Szembeni ellenállás meghatározása ACS Hurwitz kritériumnak.
Hurwitz kritérium # 150; Ez a kritérium formájában meghatározó, amely álló együtthatók a karakterisztikus egyenlet.
Átviteli függvénye az ACS (zárt helyzetben):
Az átviteli függvény megadott ACS (zárt állapotban).
szükséges és elégséges feltétele a stabilitást a automatikus ellenőrző rendszer, úgy, hogy amikor egy 0 0, az összes diagonális kiskorúak a Hurwitz determinánsok pozitív volt.
Mi található a karakterisztikus egyenlet adott rendszer.
Egyenlővé nullára nevező az átviteli függvény adott ACS:
Mi eltávolítja a zárójelben, bemutatjuk ezeket, és írjon a karakterisztikus egyenlet formájában elfogadta a rekordot:
Jelöljük az együtthatók az egyenlet, és megtalálja a jelentésük:
A mi jelöléssel a karakterisztikus egyenlet a következő lenne:
Hurwitz meghatározó össze, írja a stabilitási feltétel és stabilitásának meghatározására az automatikus ellenőrző rendszer.
Szabályzat elkészítése a meghatározó:
- Vannak írva az átlós együtthatók a karakterisztikus egyenlet, kezdve egy 1,
- Táblázat oszlopai, a fő átlós töltik fel együtthatók a karakterisztikus egyenlet növekvő indexek csökkenő le,
- Minden együtthatók indexek kisebb, mint nulla, és nagyobb mint n helyébe nullákkal (n # 150; mértéke karakterisztikus egyenlet).
ACS ellenőrizni fogja ezt ezekkel a szavakkal:
Ez az automatikus ellenőrző rendszer nem stabil, mert feltételeket a stabilitási kritérium nem teljesül.
A bizonytalanság az automatikus vezérlő rendszer látható nem csak a grafika, hanem a kritérium Hurwitz.
- Annak vizsgálatára, hogyan befolyásolja az átviteli együttható (=) A rendszer stabilitásának: meghatározni az erősítés értéke (), és segítenek megtalálni a régió stabilitását (instabilitás). Vegyük ki a grafikus átviteli függvények stabil és instabil módok és a stabilitás a határ.
Effect átviteli k együtthatót megjelenésében átmenet jellemzőit és tulajdonságait az ACS.
Simulink-modell a ACS «MATLAB» különböző k értékeket.
Effect együttható k. A tranziens válasz az ACS:
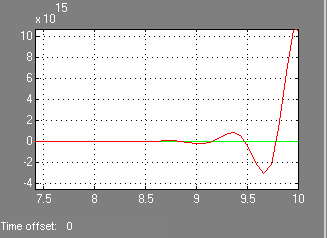
Növelésével az átviteli együttható k növeli a frekvenciát és az oszcilláció amplitúdója egy instabil rendszer.
Frekvencia és pulzus jellemzői a folyamat:
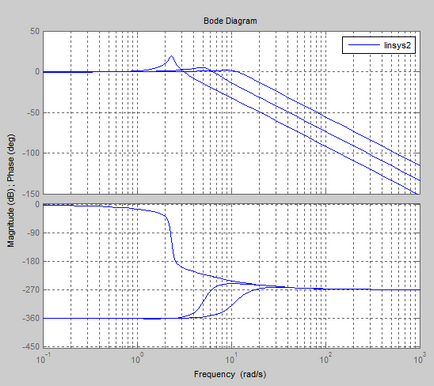
Logaritmikus amplitúdó-frekvencia és fázis válasz (Bode diagram)
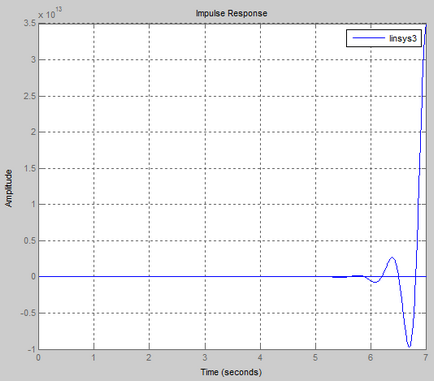
együttható k van egy határérték, ahol csökkenő k értékeket a határhoz képest rendszer stabil, miközben növeli instabil.
FIELD a rendszer stabilitását a tartománya 0 és .
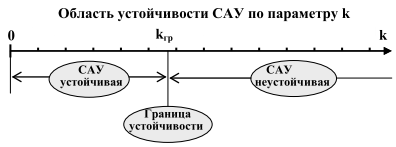
Meghatározása határérték együttható k c.
Feltételek megtalálása előre meghatározott SAU a stabilitási határ ()
Mivel arra a következtetésre jutottunk, hogy ez nem egy stabil rendszer.
A blokk diagramja az automatikus ellenőrző rendszer a stabilitási határt.
Simulink-modell az ACS stabilitására határ «MATLAB»:
Tranziens válasz az ACS stabilitására határ grafikus formában:
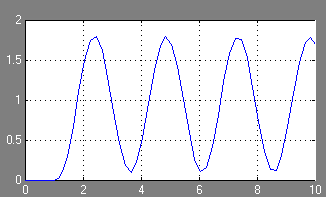
Frekvencia és pulzus jellemzői a folyamat:
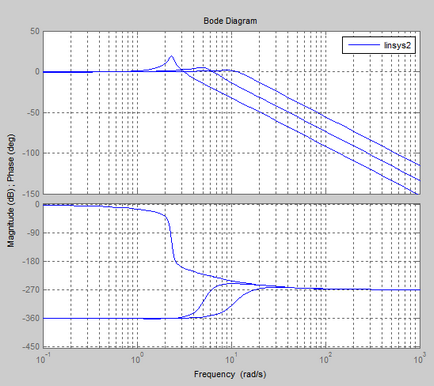
Logaritmikus amplitúdó-frekvencia és fázis válasz (Bode diagram)
Figyelembe előre meghatározott ACS biztosított
A blokkvázlata a vezérlő rendszer.
Simulink-modell az ACS amikor «MATLAB»:
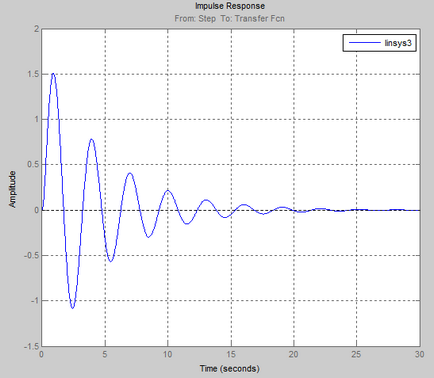
Az a lépés válasz a vezérlő rendszer grafikusan:
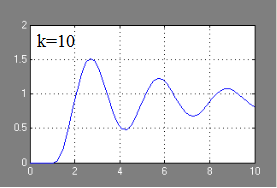
A tranziens válasz a grafikon azt mutatja, hogy egy stabil rendszer.
Frekvencia és pulzus jellemzői a folyamat:
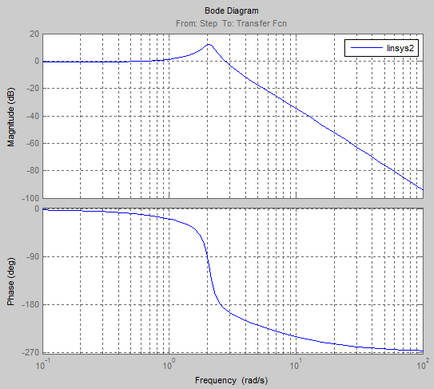
Logaritmikus amplitúdó-frekvencia és fázis válasz (Bode diagram)
Figyelembe előre meghatározott ACS biztosított
A blokkvázlata a vezérlő rendszer.
Simulink-modell az ACS amikor «MATLAB»:
Az a lépés válasz a vezérlő rendszer grafikusan:
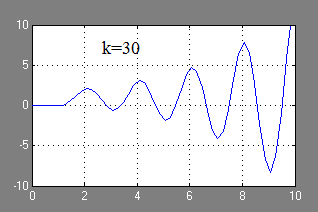
A tranziens válasz grafikon azt mutatja, hogy a rendszer instabil.
Frekvencia és pulzus jellemzői a folyamat:
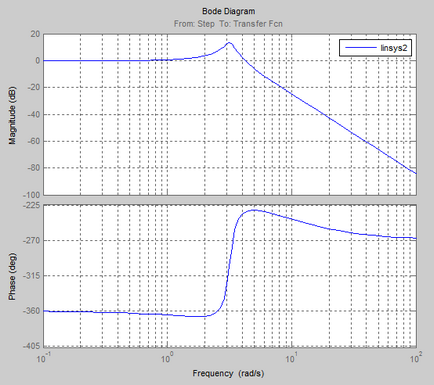
Logaritmikus amplitúdó-frekvencia és fázis válasz (Bode diagram)
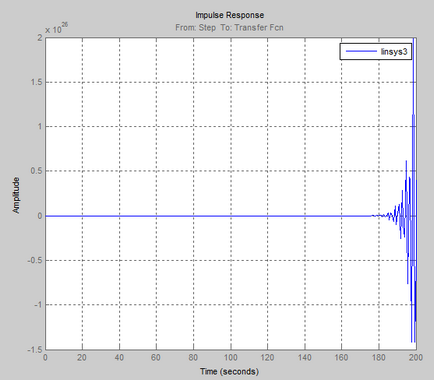
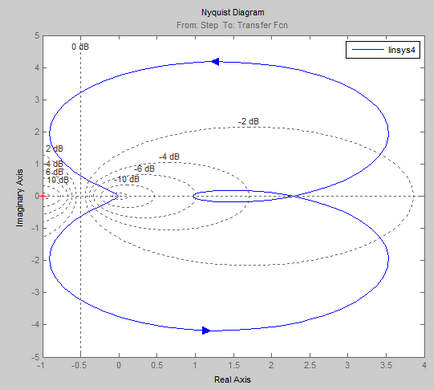
- Összehangolása modell alapjel időállandója az átviteli együttható T 3 és vizsgálja meg a rendszer stabilitását: meghatározza a határ értékeket az idő állandó T 3 és segítenek megtalálni a régió stabilitását (instabilitás). Vegyük ki a grafikus átviteli függvények stabil és instabil üzemmódok és a fenntarthatóság határait.
A hatás a rendszer stabilitásához
Befolyásolja a T időállandó 3 formájában a tranziens válasz, és tulajdonságait az ACS.
Simulink-ACS ebben a modellben «MATLAB» különböző értékű T 3.
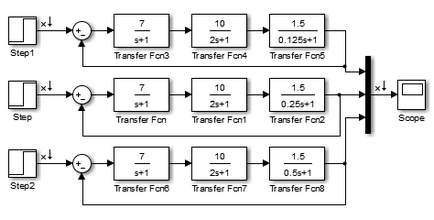
Effect 3. A T időállandó a tranziens válasz az ACS:
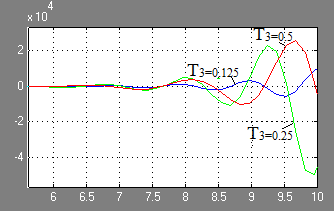
Meghatározása határ értékek T időállandó 3g.
Vegyünk egy ismeretlen paraméter T 3G és írjuk be a stabilitási feltétel határ:
Ezért azt kifejezni T 3g.
Ez a két érték a T 3G jellemzik a stabilitását határa ACS.
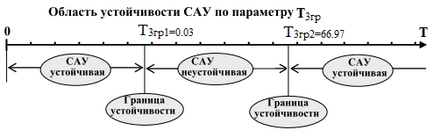
A blokkdiagramja automatikus vezérlő rendszer a stabilitási határ a T = 66,97 3g.
Simulink-modell a SAU a stabilitási határnál T = 66,97 3G «MATLAB»:
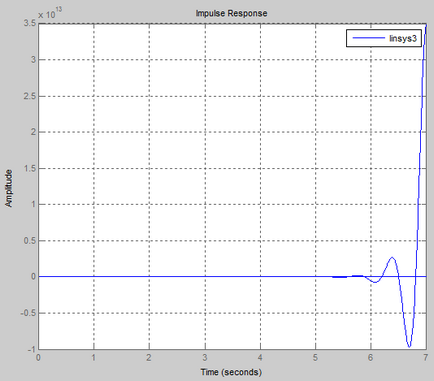
A ugrásválasz az automatikus ellenőrző rendszer a stabilitási határ a T = 66,97 3g grafikusan:
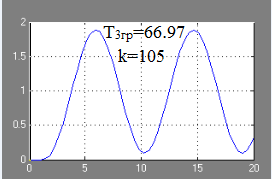
Frekvencia és pulzus jellemzői a folyamat:
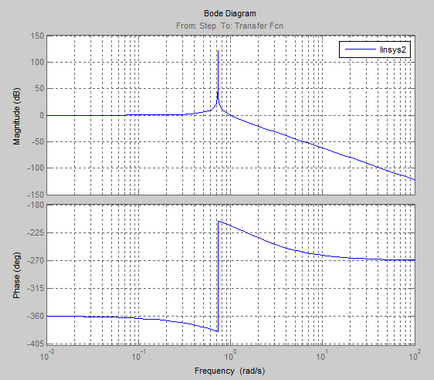
Logaritmikus amplitúdó-frekvencia és fázis válasz (Bode diagram)
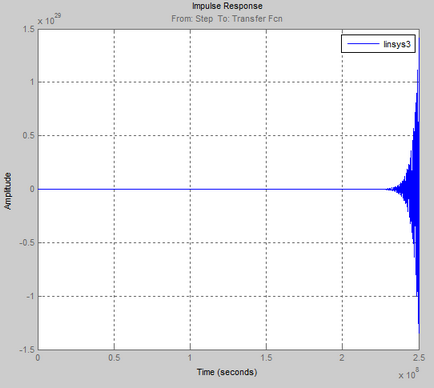
A blokk diagramja az automatikus ellenőrző rendszer a stabilitási határt 3g T = 0,03.
Simulink-modell a SAU a stabilitási határnál T = 0,03 3g «MATLAB»:
A ugrásválasz az automatikus ellenőrző rendszer a stabilitási határ a T = 0,03 3g grafikusan:
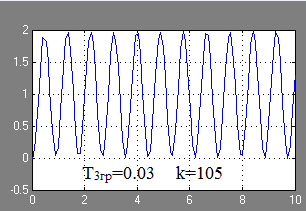
Frekvencia és pulzus jellemzői a folyamat:
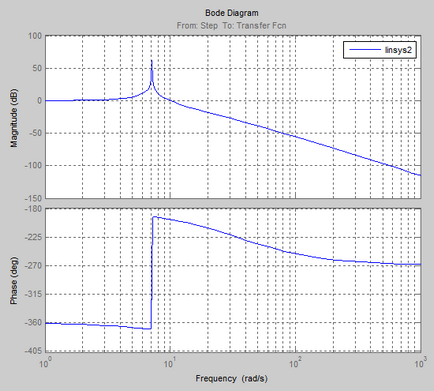
Logaritmikus amplitúdó-frekvencia és fázis válasz (Bode diagram)
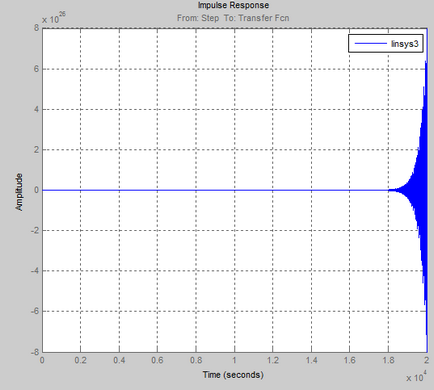
Figyelembe előre meghatározott ACS biztosított
A blokkvázlata a vezérlő rendszer.
Simulink-modell az ACS amikor «MATLAB»:
Az a lépés válasz a vezérlő rendszer grafikusan:
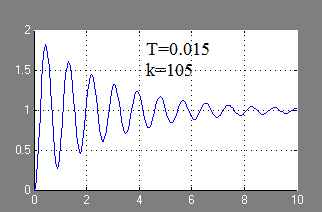
Az értékek T kisebb, mint a T 3gr1 ACS stabillá válik.
Frekvencia és pulzus jellemzői a folyamat:
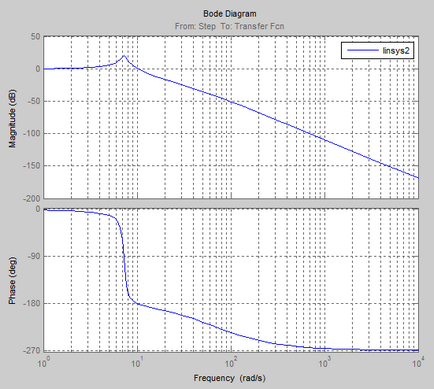
Logaritmikus amplitúdó-frekvencia és fázis válasz (Bode diagram)
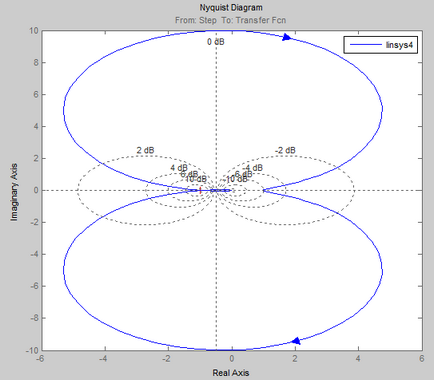
Figyelembe előre meghatározott ACS biztosított
A blokkvázlata a vezérlő rendszer.
Simulink-modell az ACS amikor «MATLAB»:
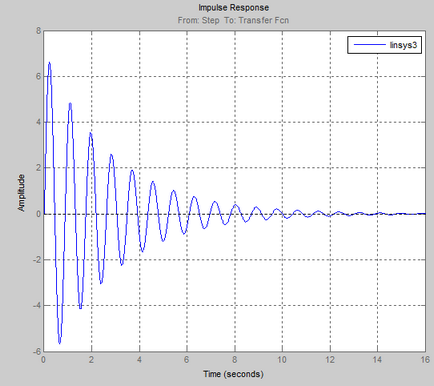
Az a lépés válasz a vezérlő rendszer grafikusan:
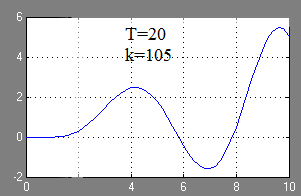
Értékek esetén T a két határ értékeket ACS instabillá válik.
Frekvencia és pulzus jellemzői a folyamat:
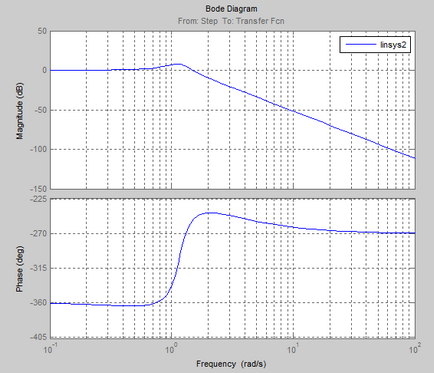
Logaritmikus amplitúdó-frekvencia és fázis válasz (Bode diagram)
Figyelembe előre meghatározott ACS biztosított
A blokkvázlata a vezérlő rendszer.
Simulink-modell az ACS amikor «MATLAB»:
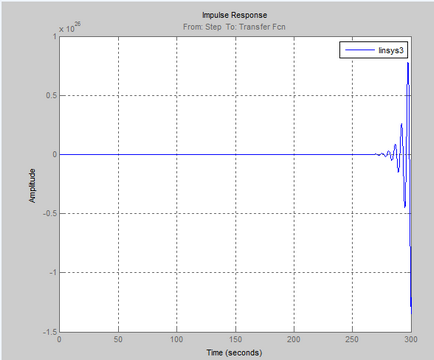
Az a lépés válasz a vezérlő rendszer grafikusan:
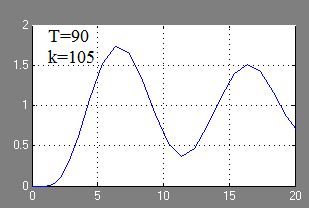
Az értékek a T, nagy T 3gr2 ACS stabillá válik.
Frekvencia és pulzus jellemzői a folyamat:
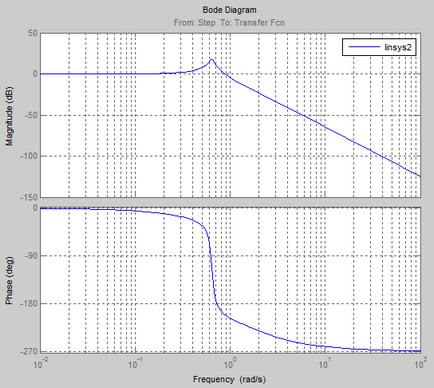
Logaritmikus amplitúdó-frekvencia és fázis válasz (Bode diagram)
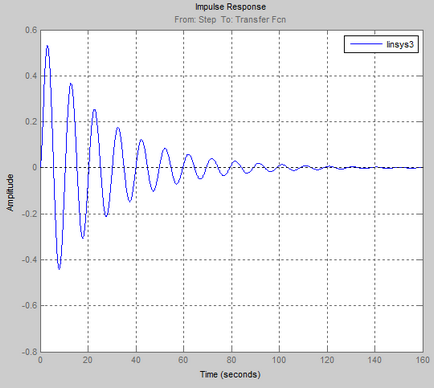
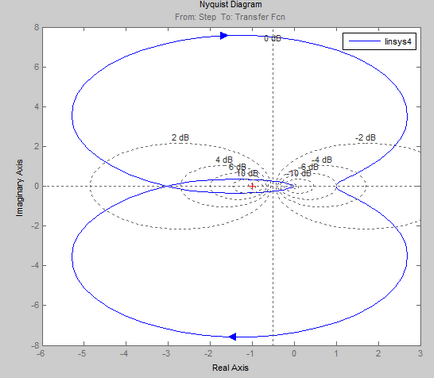
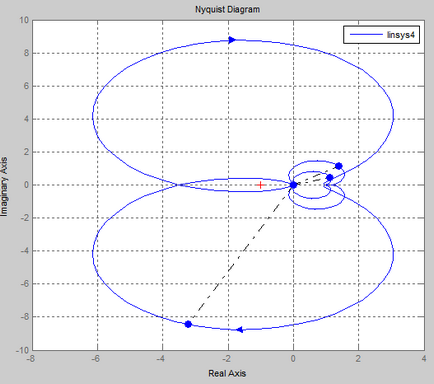
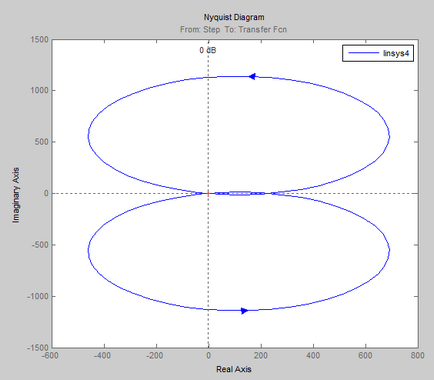
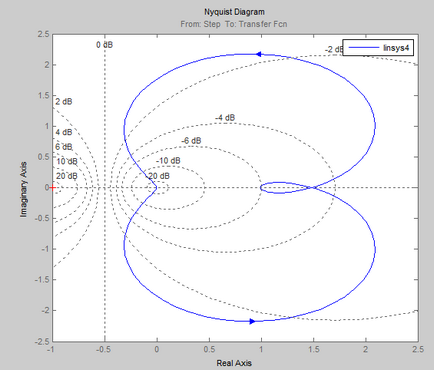
- Távolítsuk el a frekvenciamenet egy adott ACS nyitott helyzetben, és neki, hogy ellenőrizze a stabilitást a Nyquist ráta rendszert.
Stabilitási feltétel Nyquist célja, hogy meghatározzuk a stabilitását a zárt rendszerek frekvencia karakterisztika egyenértékű, hogy nyissa áramkörök.
Ha a nyílt hurkú rendszer stabil, akkor a stabilitás, a megfelelő zárt hurkú rendszer megköveteli, hogy APFC nyitott áramkör nem tartozó pont [-1, 0] a komplex síkban.
Szerkezeti felépítése az automatikus vezérlő rendszer a nyitott helyzetben.
Simulink-modell az ACS nyitott helyzetben a «MATLAB»:
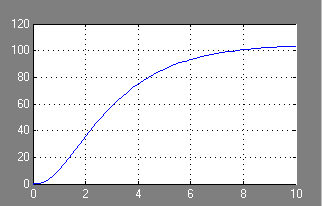
Tranziens válasz az ACS nyitott helyzetben grafikus formában:
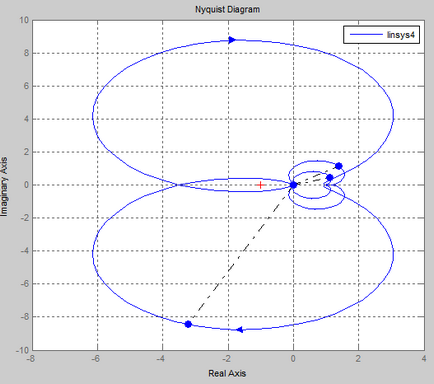
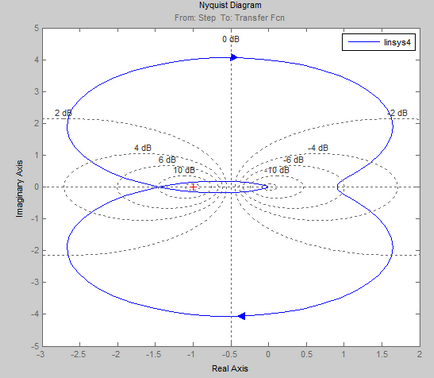
Ellenőrizzük a stabilitás az automatikus ellenőrző rendszer a Nyquist kritériumot.
A Mathcad programot.
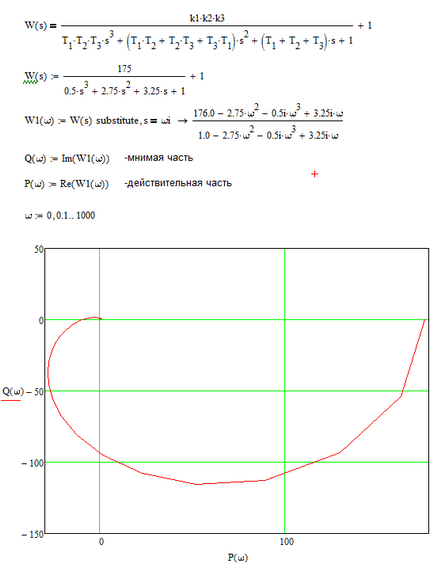
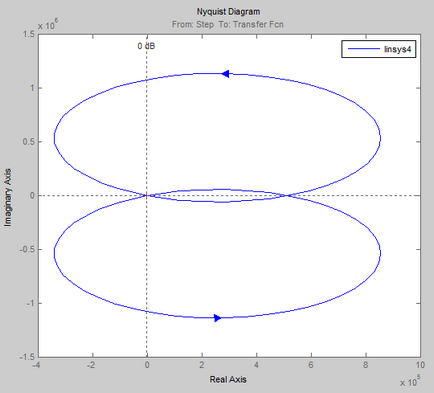
By kapott APFC rendszer, ha változik a 0-ig nyitott állapotban lehet következtetni, hogy a zárt SAU # 150; instabil, mert APFC kiterjed a pont (1; 0).
Irodalom: