A metszéspontja az átlók a paralelogramma középpontja szimmetria
Tétel: A metszéspontja az átlók a paralelogramma közepén szimmetria.
Hagyja, GR és HS - átlós paralelogramma GHRS, metszik pont A.
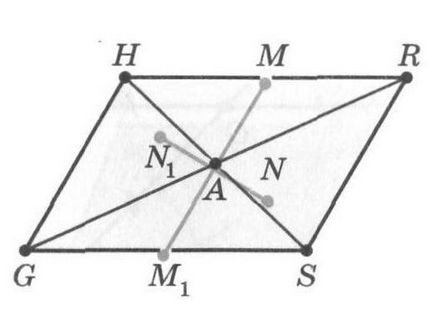
Legyen M - tetszőleges pont határán egy paralelogramma, például oldalán HR. Talál egy pontot szimmetrikus az M pont tekintetében az A. pontban Ehhez egy sugár MA, amely keresztezi a ponton oldalán GS M1. Háromszögek AMR és AM1 G egyenlő, mivel ezek egyenlő szögek és MAR M1 AG, MRA és M1 GA, valamint a része az AR és az AG.
Tehát AM1 - AM. Ez azt jelenti, hogy a pontok M és M1 egyenlő távolságra pont A. Ezért M1 - a pont középen szimmetrikus pont M a pont A. Így minden olyan M pont a határ a paralelogramma központilag szimmetrikus pont is fekszik a határán paralelogramma. Most már egyértelmű, hogy ha veszünk egy tetszőleges belső pontja N GHRS paralelogramma, akkor pont az N1. szimmetrikus hozzá képest az A ponthoz is van egy belső pontja a paralelogramma. Tehát a metszéspontja az átlók a paralelogramma A GHRS van a közepén a szimmetria.
Mint egy paralelogramma - centrálisan szimmetrikus alakja, akkor az ő véleményét - egy téglalap és rombusz, és ezért az a fajta rombusz - a tér központi szimmetrikus alakzatokat.
A szimmetriatengely és cent szimmetria síkidomok
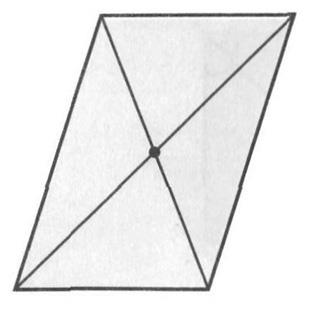
Tehát egy paralelogramma középpontja van szimmetria:
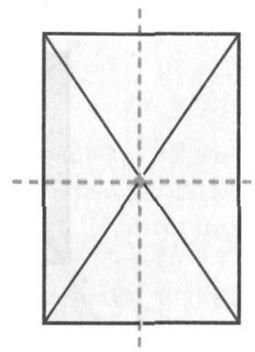
A téglalap van egy középpontja szimmetria és a két szimmetriatengelye:
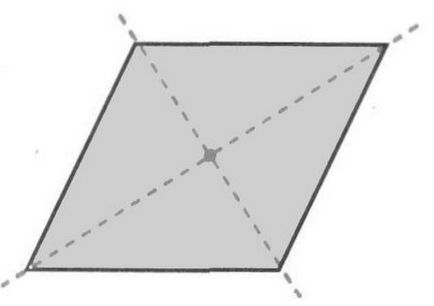
Rombusz van egy központja szimmetria és a két szimmetriatengelye:
A tér közepén egy szimmetria és a négy szimmetriatengelye:
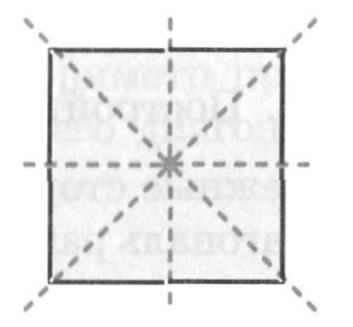
Most már tudja a különböző négyszögek és alapvető tulajdonságai és jellemzői.