Unió és kereszteződés numerikus intervallumok - matematika, előadások

Tárgy: Unió és metszéspontja numerikus intervallumok
- bevezetni a koncepció unió és metszéspontjában numerikus intervallumok, megszilárdítja a koncepció numerikus intervallum tanítani építeni numerikus időközönként a koordináta tengelyen.
- fejlődésének elősegítése: a memória, a nyelv, a figyelem, a logikus gondolkodás.
- nevelés felelőssége, kitartás és az akarat, hogy elérjék a végső eredményt.
Felszerelés. interaktív tábla.
Módszerek. verbális, vizuális, hands-on.
Alapvető fogalmak. intervallum intervallum intervallum, gerenda, nyitott gerenda; unió és kereszteződés időközönként.
Típusa tanulság: a leckét, magyarázatot az új anyag.
Epigraph leckét. Egy kínai mondás szerint:
„Hallom - elfelejtem,
Látom - emlékszem rájuk,
Én - én megemészteni. "
I. Szervezeti kérdések
Megnyitja a tanár.
Ma már sok vendég,
És megmutatjuk nekik mindazt a tudást,
Mi tudjuk, és mit kell tanulni.
Mi lesz. Természetesen a probléma megoldódik
Feladatok segít jobban megtanulni.
Azt, hogy keményen dolgoznak.
Tudomány makacs és kitartó adni.
Nos, srácok, itt az ideje, hogy elkezd
A válaszok ezekre a kérdésekre ad nekem.
II. Önmegvalósítás támogatása ismeretek
1. Készült poll-talk az átadott anyag.
Minden adott egy kártyát kérdések témában vizsgált
1. Mi a neve. számszerű különbség?
2. Ha a egyenlőtlenségeket írásjeleiket <или>, nevezik őket
a) szigorú
c) laza
3. Ha a egyenlőtlenségeket írásjeleiket ≤ vagy ≥, akkor hívják őket
a) szigorú
c) laza
4. Az úgynevezett rés. időközönként?
a) a határozat egyenlőtlenség között fekvő pontok koordinátáit és és
c) egyenlőtlenség megoldás nem hazudik a pontok koordinátáit és és
5. Mi a különbség számszerű hívott. szegmens?
a) az oldat egyenlőtlenség közé szám jelzi a numerikus rés
c) a megoldás a egyenlőtlenség nem tartalmazza a számokat, azt jelzi, hogy a numerikus intervallum.
6. Hogyan kijelölni egy koordináta pontot egy egyenes vonal, amelynek koordinátái nem a megoldás az egyenlőtlenség
a) pont festék alatt
c) egy kis kör
7. A kijelölt pont a számegyenesen, amelynek koordinátái a megoldás az egyenlőtlenség
a) pont festék alatt
c) nem átfest pont
8. Mi haszna zárójelek jelölik numerikus intervallumok
a) zárójelben
c) zárójelben
c) kerek és szögletes
2. Matematikai diktálás.
1. Írjuk be a közötti egész számok:
a) [-5; 2] b) (-6; 4)) [-7; 6) d) (-3; 4]
2. Vedd és jelölje meg a számszerű adatok hiánya miatt:
a) az intervallum 1-től 4
b) 1 és 4 közötti
c) intervallum 1-4, beleértve a 4
g) a gerenda -∞do 5
3. Írja le a rés formájában egyenlőtlenséget:
4. Rajzolj egy egyenes vonalat koordinátakészlet számok, amelyek megfelelnek az egyenlőtlenséget:
a) 5 x ≥- b) ≤3 x c) x> 7 g) X<-4 д) -4 <х<4
III. „A kereszteződés és a szakszervezet a numerikus intervallumok”
Két számszerű különbség köztük lehet „átfedés”, „merge” vagy kereszteződés lehet ∩ «üres» beállítva. Metszi a két szám lehet: intervallum intervallum intervallum.
[- 2; 4] ∩ [1; 6] = [1; 4]
Két numerikus rés nem fedik egymást. Ezután a kereszteződés numerikus intervallumok
[-4; 1] ∩ [3, 7] = az üres halmaz.
Ötvözi a két numerikus időközönként.
Minden szám az intervallum [-2; 6] tartozhat legalább egy a rések
[-2; 3] vagy [1; 6], vagy mindkettő hiányosságok. Az intervallum [-2; 6] az úgynevezett Unió térköz. Ez jelöli, [-2; 3] U [1; 6] = [-2; 6]
IV. A munka a konszolidáció az anyag
Feladat. Döntetlen a meghatározott időközönként a koordináta tengelyen. A kereszteződés és a szakszervezet időközönként. Rekord:
A tanár felolvassa a mottója a leckét, és felteszi a kérdést: „Hogyan érti a szavát a mottó?
A diákok és a vendégek kifejtsék véleményüket.
VII. Házi feladat.
P. 226 №991 (3,4); №992 (3,4)

Lecke Tárgy: „Az unió és a kereszteződésekben a numerikus időközönként”

- bevezetni a koncepció unió és metszéspontjában numerikus intervallumok, megszilárdítja a koncepció numerikus intervallum tanítani építeni numerikus időközönként a koordináta tengelyen.
- fejlődésének elősegítése: a memória, a nyelv, a figyelem, a logikus gondolkodás.
- nevelés felelőssége, kitartás és az akarat, hogy elérjék a végső eredményt.

Epigraph leckét. „Hallom - elfelejtem, látom - emlékszem rájuk, én - én megemészteni.”

Ismétlés az anyag: 1. Mi a neve. számszerű különbség?
Sokasága számok között elrendezett és b számok, az úgynevezett egy numerikus intervallum.

2. Ha a egyenlőtlenségek írásjeleiket. nevezik őket
- a) szigorú
- c) laza

3. Ha a egyenlőtlenségeket írásjeleiket ≤ vagy ≥, akkor hívják őket
- a) szigorú
- c) laza

4. Az úgynevezett rés. időközönként?
- a) a határozat egyenlőtlenség között fekvő pontok koordinátáit és és
- c) egyenlőtlenség megoldás nem hazudik a pontok koordinátáit és és

5. Mi a különbség számszerű hívott. szegmens?
- a) az oldat egyenlőtlenség közé szám jelzi a numerikus rés
- c) a megoldás a egyenlőtlenség nem tartalmazza a számokat, azt jelzi, hogy a numerikus intervallum.

6. Hogyan kijelölni egy koordináta pontot egy egyenes vonal, amelynek koordinátái nem a megoldás az egyenlőtlenség
- a) pont festék alatt
- c) egy kis kör

7. A kijelölt pont a számegyenesen, amelynek koordinátái a megoldás az egyenlőtlenség
- a) pont festék alatt
- c) nem átfest pont

8. Mi haszna zárójelek jelölik numerikus intervallumok
- a) zárójelben
- c) zárójelben
- c) kerek és szögletes

Vedd közötti egész számok:
- a) [-5; 2] b) (-6; 4)) [-7; 6) d) (-3; 4]

Vedd és jelölje meg a számszerű adatok hiánya miatt:
- a) az intervallum 1-től 4 b) 1 és 4 között) az intervallum 1-4, beleértve a 4 g) gerenda a -∞do 5

Jegyezzük fel a rés formájában egyenlőtlenséget:

Rajzolj egy egyenes vonalat a koordinátakészlet számok, amelyek megfelelnek az egyenlőtlenséget:
- a) 5 x ≥- b) ≤3 x c) x 7 g) X
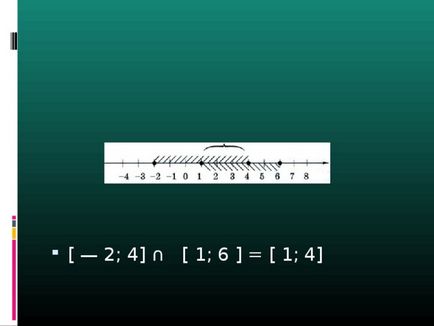
- [- 2; 4] ∩ [1; 6] = [1; 4]

- [-4; 1] ∩ [3, 7] = üres halmaz fog

- [-2; 3] U [1; 6] = [-2; 6]

Döntetlen a meghatározott időközönként a koordináta tengelyen. A kereszteződés és a szakszervezet időközönként. Rekord:
- a) (1, 7) és a (4, 9) b) [-5; 5] és [-3, 7] c) [-5, 0) és (-2, 4] d) (-4, 1), és [5; 6]

