Textbook «Scilab
Előadás 5. optimalizálási problémák
Ez leggyakrabban a mérnöki gyakorlatban osztály a problémák. Sőt, a telepítés műszaki, technológia vagy eljárás, arra törekszünk, hogy minimálisra csökkentsék valamilyen költség vagy teher, hogy maximalizálják a pozitív hatásokat, a legnagyobb utat, hogy csökkentsék a termelési ciklus, vagy éppen ellenkezőleg, hogy növelje meg annak érdekében, hogy a legjobb minőségű A termék paramétereit.
Ügyeljen arra, hogy milyen jelzőket használnak: a legnagyobb, maximum, minimum, ez a legjobb. Ezek mind leírják az optimalizálási probléma. Gazdasági számítások - még igen gyakran a megoldás az ilyen problémákra, amelyek közül néhány már klasszikussá vált. Például, a probléma a források elosztása, az utazó ügynök probléma.
Azt hiszem, nyilvánvaló, hogy a probléma ebben az osztályban nagyon változatosak, és ezért szükségessé alapvetően eltérő megközelítéseket. Tiszteletére Scilab kell jegyezni, hogy van egy megfelelő eszköztár megoldására optimalizálási problémák, megismerkedni, amellyel most viszont.
Helyi minimum egyváltozós függvényeket
Mint egy egyszerű optimalizálási probléma, úgy keresi a lokális minimum függvényében egy változó. A probléma az, hogy megtaláljuk a helyi minimum pont koordinátái meghatározott feladatokat.
Mivel ez a helyzet a keresést a gyökereit nemlineáris egyenletet, az oldatot végzett két szakaszban történik. Először meg kell felhívni a grafikon igazolja a minimum, és válassza első megközelítésben a kívánt pontra az abszcissza. Ezután az aktuális érték a koordinátákat a minimális pontot.
Vegyünk egy konkrét példát.
Keresse meg a minimum
f (x) = x4 + 3x 3 -13x 2 -6x + 26
Épület egy függvény grafikonját egy tetszőleges intervallumban. amelyet azután szükség esetén módosítani kell.

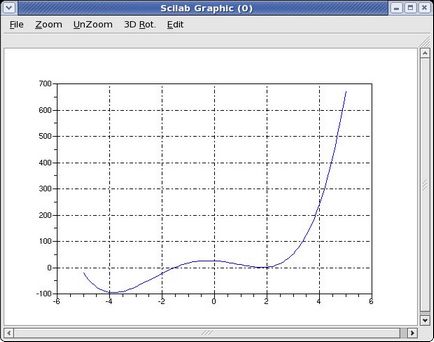
Látható, hogy a függvénynek két helyi minimumok, de egy vizuális reprezentációja van értelme vizsgálni a viselkedését a funkciót egy kisebb tartományt. mint a „farok” az a jobb oldali grafikonon kevés információ.

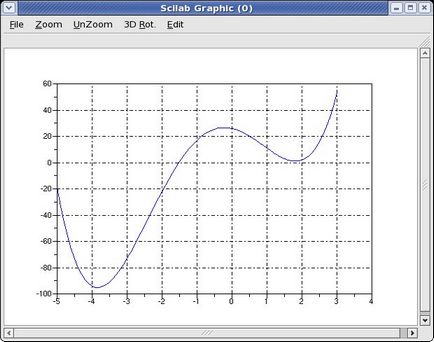
Most jól látható minimális pontot. Az első az, hogy a környéken -4, második - körülbelül 2. Annak érdekében, hogy megtalálják a pontosabb értékét a minimális funkció Scilab parancs használható
Ekkor x0 - első megközelítésben. optim parancs az abszcissza a minimális pont xmin és a függvény értéke ezen a ponton fmin. A fő jellemzője a csapat optim a szerkezete a fő érv - szórakoztató funkciók.
Tegyük fel, hogy az f (x). legalábbis ha keresünk, adott deff parancs vagy tervezési funkció (úgy, ahogy van, mert mi épült a menetrend). Ezután a szórakoztató definíciója a következő:
funkció [Fmain, Fdif, ind] = fun (x, ind)
A funkció szórakoztató. ily módon ismét a funkciót is, és annak származéka Fmain Fdif. Paraméter ind nem térünk: ez egy belső lehetőség, és azt kell kommunikálni Scilab fun optim csapat.
Most ezt az információt használja a problémát.
Most azt látjuk, az értékek minimális pontokat a korábban tisztázott első megközelítésben.

Így a mélypont ebben az esetben:
(-3,8487884; -95,889413) és (1,8068586, 1,0725284).
Hangsúlyozzuk, hogy a fő probléma a választás az első közelítés. De ez a probléma nem Scilab csomagot, és a matematikai.
Megjegyzendő, hogy amikor meghatározza a funkciót és szórakoztató Fmain Fdif közvetlenül is megadható, de ugyanakkor előfordulhat, hogy kiszámítja a származékos már más kérdés, hogy ebben az esetben ez nem nehéz.
Az eredmény természetesen ugyanaz:

Legalább Rosenbrock funkció
Térjünk át a nehezebb feladat -, hogy megtalálja a minimális funkciók több változó. Mert határozottságot, fogunk beszélni a függvény két változó.
Formális megközelítése a megoldás nem nagyon különbözik a bemutatott az előző részben. Meg kell csak figyelembe kell venni, hogy most az állítás nem egy változó, és a vektor x, a két elemből álló X (1) és X (2).
Példaként vegyük a keresést a legkisebbet Rosenbrock funkció
Ez egy ismert funkciója miatt specificitás használunk vizsgált minimalizálására algoritmusok.
Elkezdjük döntés, természetesen, az építési ütemtervet.
Építése háromdimenziós diagramok
Függvény grafikonját két definiált változók, mint ebben az esetben explicit módon, a legegyszerűbb módja annak, hogy építsenek a surf csapat.
A kód nagyon egyszerű. Először is, mi meg a tartományban érvek keresztül meshgrig csapat. az úgynevezett grid. Akkor a függvény értékek számítása a csomópontok a rács, és ha helyesen tette, surf csapat adja a kívánt eredményt.
Felhívjuk figyelmét, hogy mivel az x és y az oszlopok, a rögzítési funkció kell használni elemenként lépéseket. A mi esetünkben ez Hatványozás „^”
A grafikon a formája:
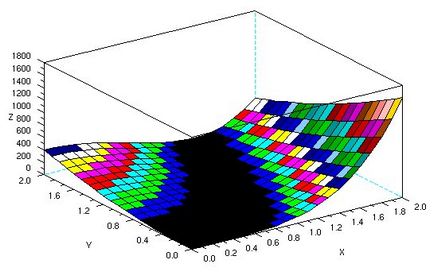
Ez nem függvénye az egyik érv, grafikusan talál legalább ő sokkal nehezebb, azonban a színe is látható, hogy a kiválasztott területen, akkor van értelme, hogy nézd meg legkevésbé. Ezért arra kérjük kiindulási pontig (0, 0), mivel a közelben ezen a ponton a legtöbb fekete.
minimum keresése
Az első megközelítésben van kiválasztva, megy a közvetlen meghatározását a minimális pontot. A könnyebb programozás átírási funkció Rosenbrock Scilab «szempontjából.”
Mivel a függvény nem egy változó, és a vektor, könnyebb meghatározni működésében design:
Mivel már használt számok, nem érték oszlopok, akkor egy közönséges hatványozást.
Mi határozza meg a Fn pontosan ugyanúgy, mint mi abban az esetben, egyváltozós függvényeket.
Mi egy kezdeti becslés, és megtalálja a minimális pontot:

Így Rosenbroke függvény minimuma van az a pont (1; 1) értéke 0. Az eredmény megfelel az elméleti. Scilab birkózni egy nehéz teszt!
A probléma az étrend
Szintén gyakran a gyakorlatban felmerülő optimalizálási probléma egy lineáris programozási feladat. Ez az osztály tartalmazza a terv a feladatok, szállítási probléma, a probléma az étrend és a többiek. Példaként tekintsük a legújabb.
Hozzon létre egy diéta, hogy a kívánt állapot minimális költség.
Nyilatkozat a problémát
Let x1. x2. x3. x4 - a szükséges számú P1 termékeket. P2. P3. P4. Ezután a teljes költség az étrend
A mi feladatunk -, hogy vegye fel xi így ez a funkció minimális volt. Az alábbi korlátozások vonatkoznak az ismeretlen xi:
- aláírja korlátozás (sőt, az ismeretlen mennyiségek pozitívnak kell lennie)
Így a matematikai megfogalmazása a probléma: hogy megtalálják a változók értékét x1. x2. x3. x4. kielégítő korlátozások rendszer (2) - (5), amelyben a lineáris függvény (1) minimális lenne. A függvény L nevezzük célfüggvényt.
A probléma megoldása érdekében a lineáris programozás Scilab tervezett funkció linpro. amelynek szintaxisa:
a -, oszlopvektor együtthatók a xi az objektív függvényben; A vektor hossza természetesen egyenlő az ismeretlenek száma.
A - a mátrix együtthatók az ismeretlenek a rendszer korlátai; a sorok számát a mátrix száma megegyezik az korlátok és az oszlopok száma megegyezik az ismeretlenek száma. Minden megszorítás kell egy jel «≤». Ha az eredeti készítmény (mint a mi esetünkben) van jelen védjegy «≥», egyenlőtlenség megszorozzuk -1.
b - oszlopvektor, amely a szabad tagjai a rendszer korlátai.
ci - egy oszlopot tartalmazó vektorral az alsó határ az ismeretlen változó; hiányát jelzi [].
Cs - egy oszlopot tartalmazó vektor felső határaként az ismeretlen változó; hiányát jelzi [].
k - egy egész szám változó, az számú egyenlet egyenlő a járdára. Ez gerenda képződése során az A mátrix első venni részvény, majd az egyenlőtlenség.
x0 - az oszlop vektor kezdeti közelítések az ismeretlen értékek.
linpro függvény egy tömb ismeretlen x, a minimum érték az f függvény és egy sor Lagrange szorzók kl.
A munka linpro csapat kell csatlakoztatni eszköz quapro. Ha ez nincs telepítve, töltse le a modul scilab.org helyén, telepítse és futtassa (File - Run) rakodó fájlt quapro könyvtárban.
megoldás a problémára
Találd meg a változó értékét x1. x2. x3. x4. ahol a célfüggvény
Eléri a minimum értéket a következő korlátozások
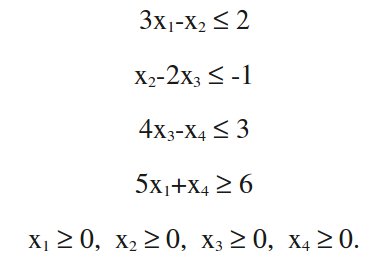
Figyeljük meg, hogy a negyedik közelítés jel „≥” meg kell változtatni, hogy „≤”, miért szaporodnak ez az egyenlőtlenség a „-1”:
Végrehajtásának megoldások Scilab jelentése:
