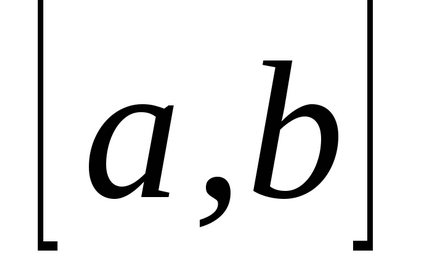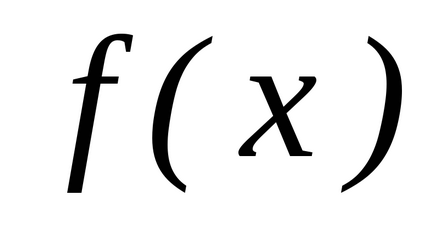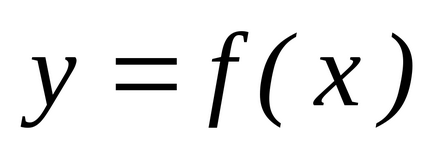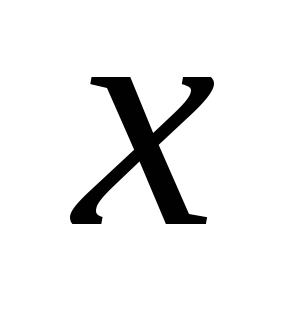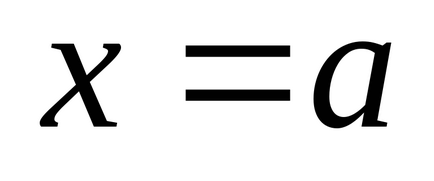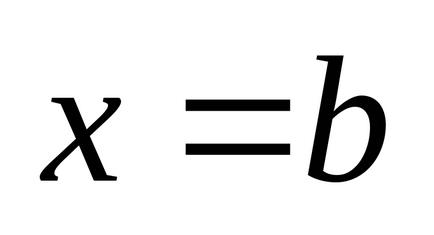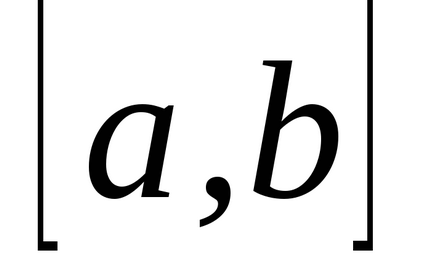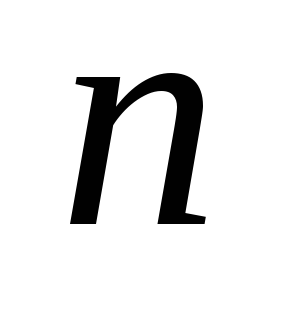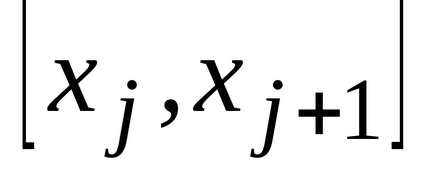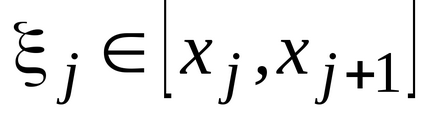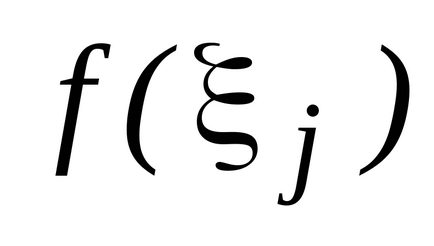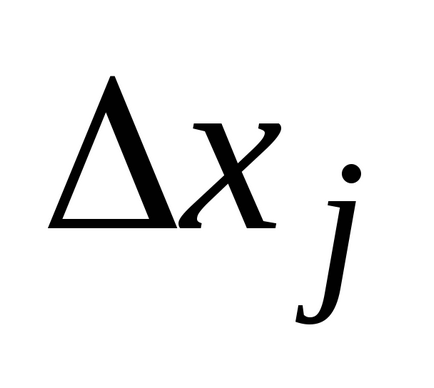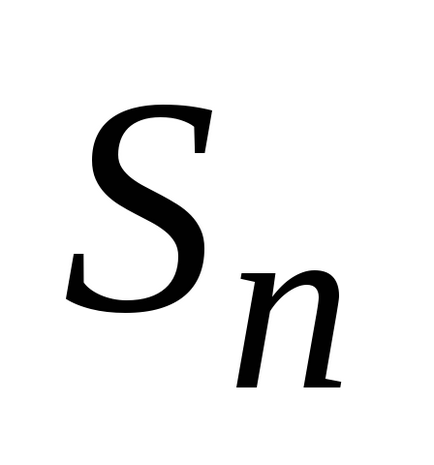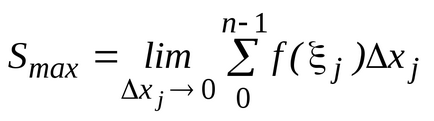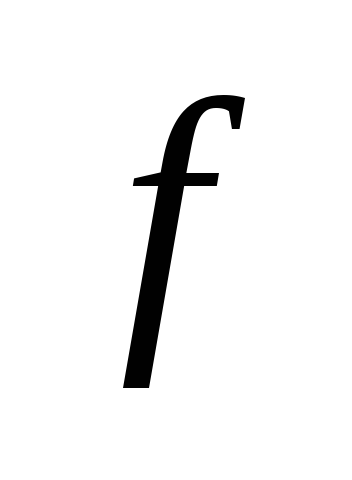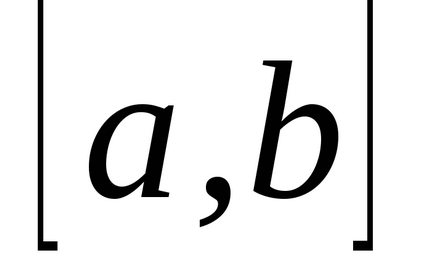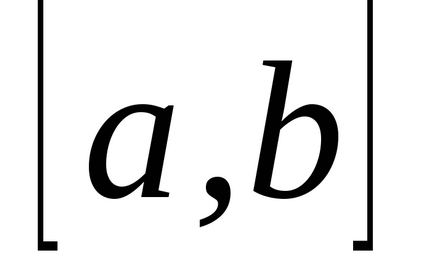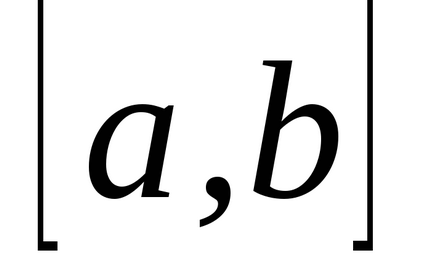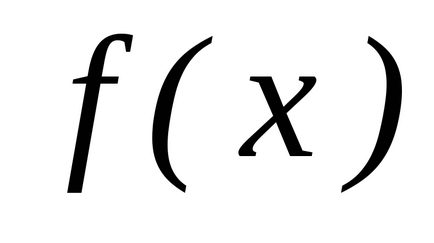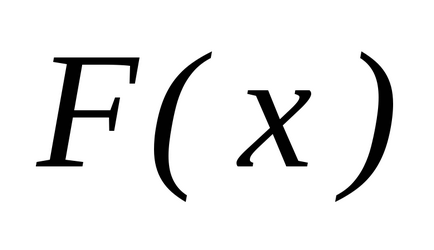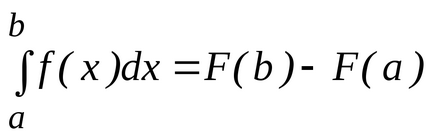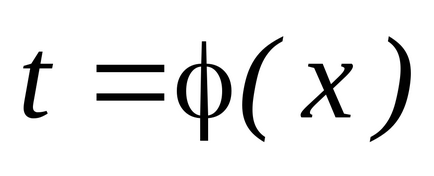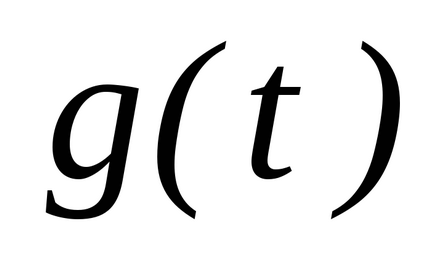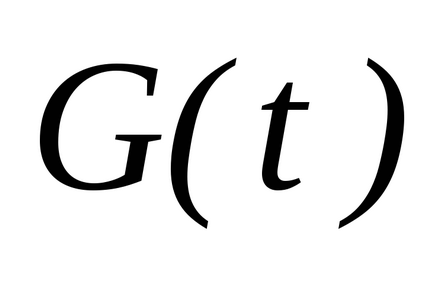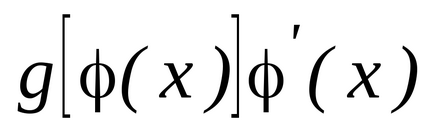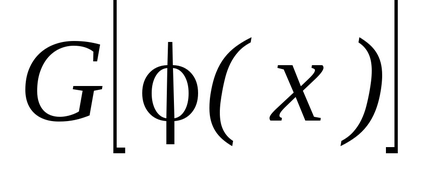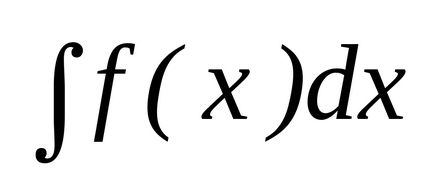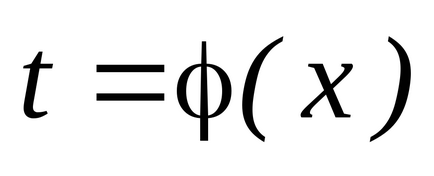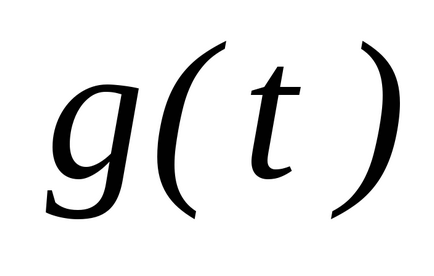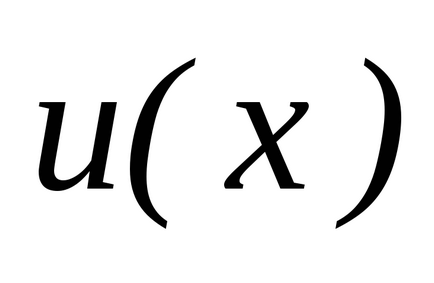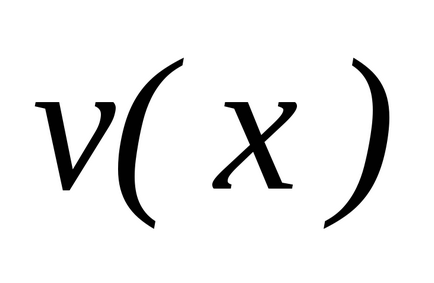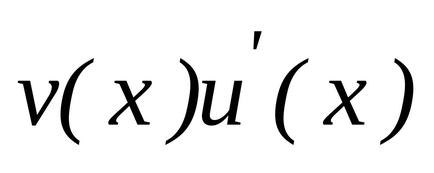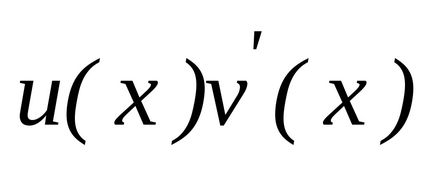Határozza meg az intervallum
(A és B - a véges számú) nemnegatív folytonos függvény
. Ábrázolják őt ütemezése és fogalmának meghatározása területén az ábra által határolt görbe
, tengely
, közvetlen
és
és ki kell számítani a környéken. Végzünk egy partíciót
tovább
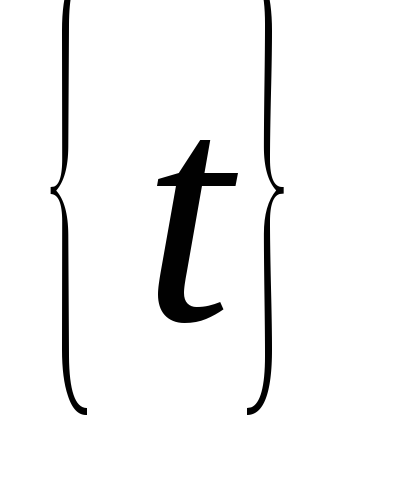
rész pont, úgy döntünk, az egyes szegmensek kapott
(J = 0, 1, ..., n-1) származó tetszőleges pont
értékeket határoz
függvény ezeken a pontokon, és kialakuljon az összeget: amely az úgynevezett szerves summoyi amely összegével egyenlő területek téglalapok. Most arra törekszünk mi
nulla, és úgy, hogy a maximális (legnagyobb) részleges otre partíció pántok általában nulla. Ha az érték a
arra törekszünk, hogy op bizonyos határig
, független módon a partíciót, és válassza ki a pontokat
. Ezután az értéke
hívja terület a mi görbe formák. Így.:
.
Rontva a működését, hogy megtaláljuk a területen, úgy véljük, ez a művelet, mint találni egy bizonyos számú
Ennek a funkciónak
, meghatározott intervallumon
:.
A határozott integrál függvény az intervallumon
Ez a határ az integrál összeg, ha a maximális részhosszán partíció megy nullára.
Adott egy folytonos
függvény
és hagyja
létesítő primitív. Tétel Newton-Leibniz állítja érvényességét a következő egyenletet:
.
Alapvető módszerek integrációját
Integrálása a változó helyettesítő (szubsztitúciós)
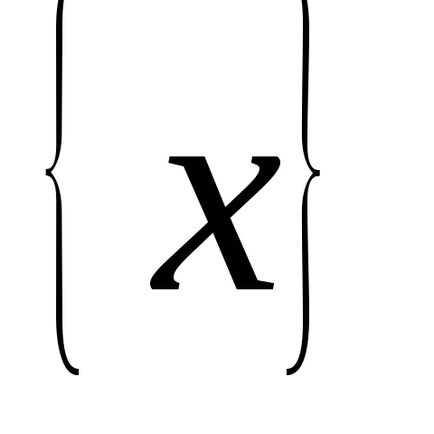
Legyen a függvény
meghatározott és differenciálható egy sor
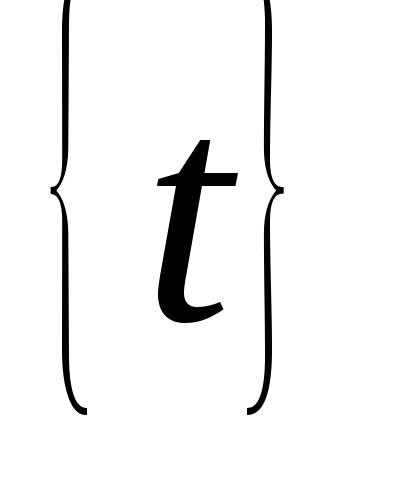
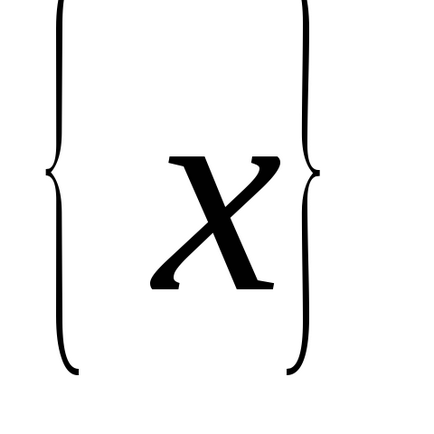
, és hagyja
A készlet minden érték ezt a funkciót. Tegyük fel továbbá, hogy a funkció
ott a forgatáson
primitív függvény
, t. e .. Aztán mindenhol
függvény
Van egy primitív függvény egyenlő
, t. e.
.
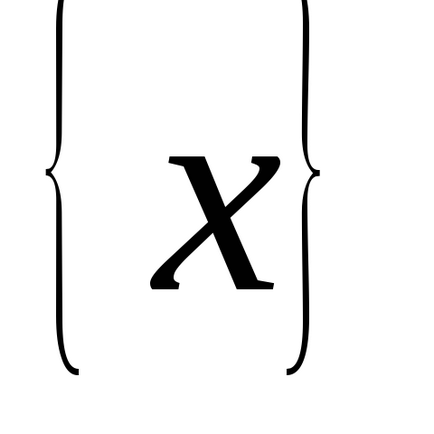
Tegyük fel, hogy szeretnénk számítani a szerves
és lehet választani, mint egy függvény egy új változó
úgy, hogy a
könnyen integrálható, azaz.:
és - ez a módszer számítási nevezett integráció helyett a változó.
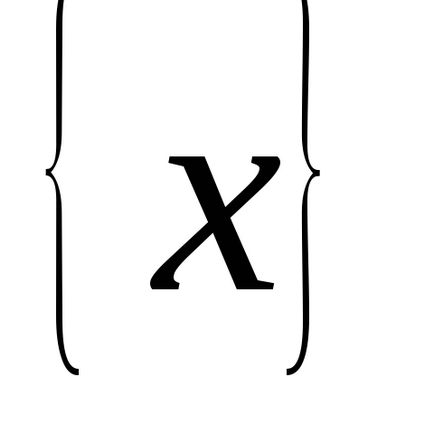
Integrálás
Hagyja az egyes funkciók
és
differenciálható
és emellett ezen halmaz van egy primitív függvény
. Aztán a forgatáson
Van egy primitív függvény
, ahol, a képlet
.
Kapcsolódó cikkek