Ezenkívül a számok a különböző jelek, matematikai
Probléma 1. Az a játékos nyer felvett egy + jel és a veszteség -. Keresse az eredmény egyes alábbi feljegyzések: a) 7 rubelt. 4 dörzsölje.; b) -3 dörzsölje. -6 dörzsölje.; c) -4 o. 4 o.; d) +8 o. -6 P.; e) -11 p. 7. o.; f) +2 o. 3 p. -5 P.; g) +6 o. -4 o. 3 p. -5 o. 2 o. -6 o.
Felvétel a) azt jelzi, hogy a játékos az első megnyert 7 rubelt. majd egy másik győzelem 4 p. - összesen nyert 11 p.; Entry c) meghatározza, hogy az első játékos elvesztette 4 p. Megnyerte majd 4 p. - mert a végeredmény = 0 (a játékos nem tett semmit); e rekord) azt jelzi, hogy a játékos először elvesztette 11 rubel. majd megnyerte 7 rubelt. - a veszteség meghaladja a nyereség 4 dörzsölje.; Ezért általában a játékos elveszti 4 rubelt. Tehát joga van ezeket a feljegyzéseket rögzíteni, hogy a
a) +7 p. 4 o. = 11 o.; c) -4 o. 4 o. = 0; e) -11 p. 7 + p. = -4 rubelt.
Azt is könnyű megérteni a többi rekordot.
Annak értelmében ezek a feladatok hasonlóak a számtani hozzáadásával oldják akciók, ezért itt most tegyük fel, hogy minden szükséges egy közös eredmény a játék, hogy a relatív számokat, hogy az eredményeket az egyes játékokat, például a példában c) a relatív száma -11 rubelt. adunk a relatív száma 7 rubelt.
Probléma 2: A pénztáros rögzített érkezése készpénz + jel, és a megjelölés a fogyasztás -. Keresse meg a végeredményt az egyes alábbi feljegyzések: a) 16 p. 24 p.; b) -17 p. -48 P.; c) +26 o. -26 P.; d) -24 p. 56 p.; e) -24 p. 6 p.; f) -3 o. 25 p. -20 p. 35 p.; g) +17 o. -11 o. 14 p. -9 o. -18 p. 7. o.; h) -9 o -7 o. 15 p. -11 o. 4 o.
Nézzük, például. Entry f): kiszámítjuk az első az egész egyházközség irodák: ezen a lemezen 25 rubel. plébánia, és még 35 rubel. Gyere összesen érkezés 60 rubel. és a fogyasztás volt 3 rubelt. és még 20 rubelt. Összesen 23 rubel. fogyasztásra; Parish meghaladja a fogyasztást 37 rubel. Köv.,
- 3 rubelt. + 25 rubelt. - 20 rubel. + 35 rubelt. = 37 rubelt.
Probléma 3. pont ingadozik egy egyenes vonal mentén az A pont (ábra. 2).
Mozgás jobbra jelezve a jelek + és mozog, hogy a bal oldalon - jel. Amennyiben pont lesz, miután több oszcilláció rögzített odnoyu a következő feljegyzések: a) 2 dm. Dm -3. 4 dm.; b) -1 dm. Dm 2. Dm 3. 4 dm. -5 dm. +3 dm.; c) +10 dm. Dm -1. 8 dm. Dm -2. 6 dm. Dm -3. 4 dm. -5 dm.; d) -4 dm. 1 dm. -6 dm. Dm 3. -8 dm. 5 dm.; e) +5 dm. -6 dm. 8 dm. -11 dm. A rajzon, kijelölt inch szegmensek, kevésbé valóságos.
Az utolsó bejegyzés (e) elemzi: első rezgő pont került az jobbra egy 5 dm. aztán a bal oldalra kerül 6 dm. - Általában meg kell megmarad maradt az 1 dm. akkor költözött a jobb oldalon a 8 hüvelyk. jelet. Most ez a jogot A 7 dm. majd a bal oldalra 11 dm. ezért a bal oldalon egy 4 dm.
A többi példa a hallgatók szétszedni magát.
Feltételeztük, hogy az összes rekordot kell tenni a szétszerelt felvett relatív számokat. Ezért vállalja, hogy:
Ha több relatív számok mellé írt (a karakter), majd ezeket a számokat kell összeadni.
Nézzük most a fő során bekövetkező események hozzáadását, és megteszi a relatív számokat név nélkül (m. E. helyett mondani, pl. 5 RUB. Win, sőt 3 RUB. Győzd vagy pont eltolt 5 dm. Jobb oldalán , de aztán újabb 3 dm. Bal, mondjuk 5 pozitív egység, akár negatív 3 db ...).
Itt kell összeadni a számokat, amely 8 Pos. egységek, és még 5 Pos. egységek, megkapjuk álló számot 13 Pos. egység.
Itt kell megállapítani álló számot 6 otritsat. az egységek számát, amely 9 otritsat. egységek így 15 otritsat. egységek (vö :. 6 rubelt veszít és veszít 9 rubel - teszi 15 rubelt veszteség.). Így
4 nyeremény rubel igen, akkor 4 rubelt. veszteség, általában, hogy a nulla (kiesnek); is, ha az A pont költözött az első jobbra 4 dm. majd balra a 4 dm. lesz újra pont, és a nyoma. végleges való távolsága A nullával egyenlő, és minden azt kell feltételeznünk, hogy a 4 Pos. egységek, és még 4 negatív, általában, hogy nulla vagy éppen törölheti. Így
+ 4 - 4 = 0, és - 6 + 6 = 0, stb ..
Két relatív szám, amelynek azonos nagyságú, de különböző jelek kioltják egymást.
6 otritsat. egység megsemmisült 6 Pos. egységek, de továbbra is 3 poz. egységet. Így
7 Pos. 7 egység megsemmisült otritsat. egységek, de továbbra is a 4. otritsat. egységet. Így
Figyelembe véve 1), 2), 4) és 5) esetek
+ 8 + 5 = + 13; - 6 - 9 = - 15; - 6 + 9 = + 3, és
+ 7-11 = - 4.
Ebből látjuk, hogy meg kell különböztetni két esetet, a mellett az algebrai számok: az esetben, ha a kifejezés ugyanazt jel (1. és 2.), és egy esetben hozzáadásával számokat különböző jelek (4. és 5.).
Most nem nehéz belátni, hogy
úgy, hogy a számok azonos védjegy kell hajtani az abszolút értékeket, és azt írja, hogy a közös jel, és hozzá két szám különböző előjelű szükséges aritmetikai kivonni az abszolút értékeket (nagyobb kisebb), és írd token száma, amelyek abszolút értéke nagyobb.
Tegyük fel, hogy meg akarja találni az összeg
+ 6 - 7 - 3 + 5 - 4 - 7 + 8 + 9.
Ezt először összeadjuk a pozitív számok + 6 + 5 + 7 + 9 = 27 +, akkor minden otritsat. - 7 - 3 - 4-8 = - 22, majd az eredményeket az egymás közötti + 27 - 22 = + 5.
Azt is kihasználják, hogy itt a száma 5 + - 4 - + 8 7 kioltják egymást, és így csak hozzá a számokat 6 + - 7 - + 3 + 5 = 9.
Egy másik módszer a felül jelölési
Minden kifejezés lehet szögletes zárójelek és a zárójelben írja a jele kívül. Ex.:
Tudjuk szerint az előző, azonnal írja le az összeget, például. (4) + (5) = 1 (az ügy hozzáadásának számok különböző jelek: legyen egy nagyobb abszolút értékű kivonni kevesebb és levelet jele, amelyben az abszolút érték nagyobb), hanem képes átírni az első azonos zárójel nélkül , kihasználva a feltétellel, hogy ha a szám mellé írt a karakterek, ezek a számok kell összeadni; köv.,
hogy nyissa ki a zárójelben, ha hozzá pozitív és negatív számokat, meg kell írni néhány szempontból, hogy a jelek (plusz jel és konzolok elhagyható).
Pl. (+ 7) + (+ 9) = + 7 + 9; (- 3) + (- 8) = - 3 - 8; (+ 7) + (- 11) = 7 + - 11; (- 4) + (+ 5) = - 4 + 5; (- 3) + (+ 5) + (- 7) + (+ 9) + (- 11) = - 3 + 5 - + 7 9 - 11.
Ezt követően, az így kapott számokat lehet hajtani.
Ennek során algebra különös figyelmet kell fordítania az a képesség, hogy nyissa ki a zárójelbe.
1) (- 7) + (+ 11) + (- 15) + (+ 8) + (- 1);
Néha, hogy néhány egyszerűsítést a kijelölését Továbbá: 1) az első félévben van írva zárójelek nélkül. Ex.:
2) A + jel az első menetek száma és az írási feszültséget. 5 + (- 7) helyett + 5 + (- 7) (lásd a végén a 10 ..).
3) A + jel is néha a menetek száma, ha azonnal írva a zárójelben. Ex.:
- 1 + (7) + (- 2) + (5) helyett - 1 + (+ 7) + (- 2) + (+ 5).
1);
2) - 0,5 + (+ 0,25) + (- 1,07) + (- 0,13);
3) 1,24 + (- 0,77) + (+ 2,35) + (- 1,575).
Itt van egy bonyolultabb példát kívül:
.
Itt is szükséges a műveletek végrehajtásához szögletes zárójelben: az egyes sávok kell hozzá írt számokat, azok mellé írt jeleik (abban az esetben felül különböző előjelű) is. Aztán ott van:
.
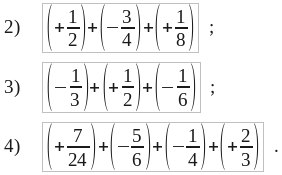
Gyakorlatokat.
1) + 1 (3 - 7) + (július 1-6 + - 8 + 9);
2) 1 + [3 + (7-11)];