A megoldás a lineáris és négyzetes egyenlőtlenségek
Ebben a leckében fogjuk megoldani a lineáris és négyzetes egyenlőtlenségek megnövekedett összetettsége. Kezdetben ne feledjük, hogy ez a lineáris és másodfokú egyenlőtlenségek. Emlékezzünk csak a módszerek és tulajdonságok oldatok másodfokú függvényt, és hogy az adatokat a táblázatban. Következő fogjuk kezelni egyenlőtlenség megnövekedett összetettsége.
Tárgy: A Rational egyenlőtlenségek és rendszerek
Lecke: megoldása a lineáris és négyzetes egyenlőtlenségek
1. meghatározása lineáris egyenlőtlenségek
Lineáris egyenlőtlenségek - egyfajta egyenlőtlenség és azokat megoldani kétféle módon: vagy azzal egyenértékű transzformációk segítségével grafikus funkciókat. Tekintsük a második módszer a példákban:
2. megoldás lineáris egyenlőtlenségek grafikusan
1. Oldja meg az egyenlőtlenséget
Építünk a függvény grafikonját. Graph egy egyenes vonal, keresztezi a Oy tengelyen a ponton 1, ökör tengely t. A gyökér funkció osztja tengely ox két különböző időközönként. Az első intervallum funkció negatív, a második - pozitív.
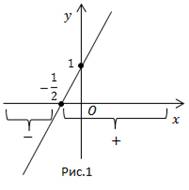
Ez elég ahhoz, hogy megoldja a lineáris egyenlőtlenség.
Lineáris egyenlőtlenségek hatékonyabban megoldható kiválasztásával milyen időközönként funkció megőrzi jel, azaz a. E. A gyökér a gyökér. Megoldás lineáris egyenlőtlenségek, mint általában, egy gerenda.
3. Döntés tér egyenlőtlenségeket grafikusan
Tekintsük a másodfokú egyenlőtlenség
Ezt úgy oldják meg, a tulajdonságok a másodfokú függvények
Tekintsük a következő példát.
2. Oldja meg az egyenlőtlenséget
Tekintsük az megépíteni a menetrend, ez a mi megtalálni a gyökereit az első. A tétel az Térség
Sematikusan ábrázolják a parabola és határozza meg a időközönként állandó jel és a jelek őket. parabola ága felfelé irányuljon.
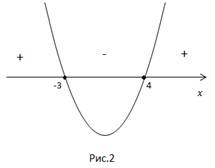
Függetlenül attól, hogy a gyökerei az intervallum pozitív, belül a gyökere az intervallum - negatív.
Tekintsük a másodfokú függvény és tulajdonságai általában.
4. A másodfokú függvény általános formában, a D> 0
Függvény formájában
átlagos másodfokú polinom gyökerek különbözőek,
A grafikon a másodfokú parabola, metsző pontok ökör tengely abszcisszavonal
parabola ága felfelé irányuljon.
Függetlenül attól, hogy a gyökerek a intervallum funkció pozitív jel, belül a gyökere az intervallum - negatív.
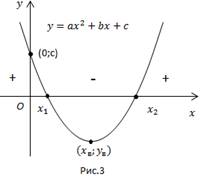
Mit lehet mondani a függvény, ha az első helyen, hogy bomlik lineáris tényező:
Térség tétel is igaz ez:
Találunk a koordinátákat a csúcsa a parabola.
A másodfokú függvény két lehetősége van az egyenlőtlenségek:
A beállított értékek a funkció - a gerenda a pozitív irányba. A metszéspontja a tengellyel Oy - t ..
5. A másodfokú függvény általános formában, a D = 0
Csakúgy, mint az előző esetben, a polinom bontjuk tényezők.
A grafikon - parabola ága felfelé irányuljon.
Parabola tekintetben ökör tengely egy ponton, ami a csúcsa a parabola.
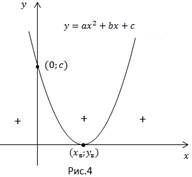
Tekintsük a lehetőségek egyenlőtlenségek:
A beállított értékek:
Funkció grafikon metszi a tengelyt Oy Vol.
6. A másodfokú függvény általános formában, a D
azt jelenti, hogy az egyenletnek nincs gyökér, trinomiális nem bontható tényezők és nem teljesül Térség tétel.
Megtaláljuk a csúcsainak koordinátáit:
Ábrák vázlatosan egy grafikon - parabola ága felfelé irányuljon.
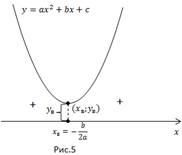
Ebben az esetben a standard hiba gyakran hagyjuk - nincsenek gyökerei, az azt jelenti, hogy nincsenek megoldások. Ez nem gyökerei egy másodfokú egyenlet, és a megoldás a egyenlőtlenség minden valós szám.
Az értékrendje
Alaposabb vizsgálat ajánlott, hogy tanulmányozza az eseteket, amikor
Meg kell építeni, grafikára standard oldatok egyenlőtlenségek függetlenül.
7. Problémamegoldás
Megvizsgáltuk részletesen tulajdonságait kvadratikus függvények, amelyek megalapozzák a problémamegoldás.
1. Keresse meg a domain a funkciót.
A tartomány a függvény által meghatározott egyenlőtlenség t. K. trinomiális alatt található a gyökér a nevezőben.
Szorozzuk mindkét oldalán egyenlőtlenséget.
Tekintsük az fogja találni a gyökerei.
A tétel az Térség
Képzeljük függvény grafikonját. 1. pontjában és -2 kilyukadt, t. K. A szigorú egyenlőtlenség.
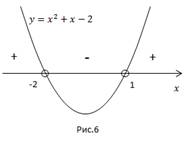
Ez megfelel a feltételeknek meg belülről a gyökér rés intervallumot.
Láttunk egy példa arra, hogy sok probléma lehet csökkenteni másodfokú egyenlet megoldása.
8. A határozat a paraméter az egyenlőtlenség
2. Amikor mi a p értéke, ez egyenletnek
két különálló gyökerek?
Ez nincs gyökere?
Ha p egy meghatározott értéket, van egy bizonyos másodfokú trinomiális fajlagos értéke a diszkrimináló,
Találunk a gyökerei a Térség tétel.
Tekintsük a p tengelye és a ütemezés funkció egy grafikon, a parabola ága felfelé irányuljon.
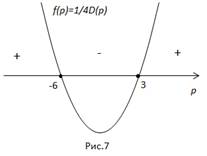
A függvény tartja a pozitív előjel a gyökere az intervallum, negatív előjellel - az intervallum.
Válasz: A egyenletnek
1. két különböző gyökerek, amikor
2. egy gyökér, amikor
3. nincsenek rendszergazdai amikor
19. Következtetések
Megvizsgáltuk a megoldás a lineáris és másodfokú egyenlőtlenségek bizonyos tulajdonságai másodfokú függvények, amelyek használják a Másodfokú egyenlőtlenség.
Az ajánlott olvasás
Ajánlott linkek az online forrásokat
1. Portal of Natural Sciences.
2. Center for Education "oktatási technológia."
3. Elektronikus oktatási és módszertani komplex előállítására 10-11 osztályok felvételi vizsgákra számítástechnika, matematika, orosz nyelven.
4. A virtuális oktató.
5. § Főiskola. ru matek.
Ajánlott házi
Loading.
Be kell, hogy töltse le a óravázlatok a témában „A megoldás a lineáris és másodfokú egyenlőtlenségek. tartás kapcsolat
Loading.
Népszerű művek
- Tájképek a dalszövegek S.Pushkina
- Elemzés Blok vers „A területen Kulikovom”
- Apa és fia a történet D. Aldridge „Az utolsó Inch”
- Élete és munkássága Goethe VI
- Döntéseket a választottbíróság. feladatok
- Tervezése vendéglátóipari tervezés étteremben. 2. rész
- A. és S. S.Pushkin A.Esenin orosz természet