Center párhuzamos erők

Home | Rólunk | visszacsatolás
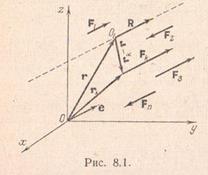
Feltételezve, hogy ez a feltétel teljesül, megtudja, mi történik a kapott közben egyszerre forognak párhuzamos adatátviteli vonalak cselekvési erők egy és ugyanazon a szöget, amikor az alkalmazás helyétől ezen erők változatlanok maradnak, és kiderül akció erővonalak előfordul párhuzamos tengelyek körül.
Ilyen körülmények között az eredő erő adott rendszer egyszerre forgatjuk azonos szögben, a forgatás körül zajlik egy fix pont az úgynevezett központja párhuzamos erők. Térjünk át a bizonyítéka ennek az állításnak.
Tegyük fel, hogy a rendszer a párhuzamos erők a kapott vektor nem nulla, ezért a rendszer erő a kapott. Hagyja, hogy a pont van olyan pont a hatóirányának kapott. Tegyük fel most, - a sugara vektor a pont képest kiválasztott pólus. és - a sugár vektor a pont az erő alkalmazása.
Szerint Varignon tétel összege az összes momentuma erők a pontrendszer nullával egyenlő:
. (8,2), mint az a pont fekszik a vonalon az eredője tevékenységének.
Ez az egyenlet átírható az alábbi formában:
Most bemutatjuk a készülék vektor. Párhuzamos vonalak erők. Ezután minden erő is képviselteti magát
hol. ha a erő irányában vektort és az azonos, és a. és ha irányított egymással szemben. Nyilvánvaló, hogy ebben az esetben
. (8.5) Behelyettesítve kifejezések (8.4) és (8.5) a (8.3), megkapjuk
Az utolsó egyenlőség elégedett bármilyen erő irányának (azaz, az irányba, egy egység vektor) csak azzal a feltétellel, hogy az első tényező egyenlő nullával:
Ez viszont egyenletnek van egy egyedülálló megoldás tekintetében a sugár vektor. meghatározunk egy pontot kapott alkalmazást, amely nem változtatja meg álláspontját forgatásával cselekvési irányok erők. Ez a pont a közepén párhuzamos erők, amelyek a létezését bizonyítja. Jelöli a központ a sugár vektor párhuzamos erők révén. re (8,7) megkapjuk
Let. . - koordinálja a központ párhuzamos erők is. . - a középpontjának koordinátáit egy tetszőleges erő alkalmazásával; akkor a középpontjának koordinátáit párhuzamos erők találtak a képletek:
az úgynevezett statikus pillanat egy adott rendszer erők adott koordináta síkon. . .
Megjegyezzük, hogy az eredete középpontjában párhuzamos erők,
valamint a statikus pillanatok egy adott rendszer teljesítmény nullával egyenlő.
A test tetszőleges alakú, mivel a gravitációs mező lehet osztani szakaszok párhuzamosak a koordináta síkok, elemi kötetek. Ha figyelmen kívül hagyjuk a szervezet mérete, összehasonlítva a Föld sugara, a gravitációs erő ható egyes elemi térfogat lehet tekinteni egymással párhuzamosan. Jelöljük kötet elemi hasáb a középpontot. és a gravitációs erő ható ez az elem - a. Azután egy átlagot fajsúlya a térfogati aránya elem. Húz egy doboz pont. Mi a fajlagos tömege egy adott ponton a test, mint a határérték az átlagos fajlagos tömege
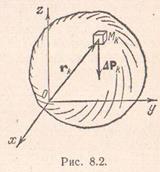
Formula (8.11) meghatározza a pozícióját egy pont.
A súlypont az a pont, amely a határ a pontokat. Más szóval, a test súlypontja az úgynevezett egy pont, amelynek sugara vektor határozza meg az alábbi határértékeket:
(8,12), illetve figyelembe véve a fajsúly,
. (8,13) Amikor ezt a korlátot feltételezzük, hogy a méretek minden parallelepipedonok általában nulla. Határértékek nevezők egyenletekben (8,12) és a (8.13) egyenlő testtömeg
Mivel a határait az integrál összegek a számláló és a nevező általános képletű (8,13) vannak definiálva integrálok át térfogata a test, akkor az alábbi képlettel ábrázolható:
Koordinátáit a súlypont által meghatározott képlet:
A test azt mondják, hogy homogén, ha. Ebben az esetben az érték kell tenni a képletek (8,14) az integrál jelek a számláló és a nevező és csökken. A nevezők egyenletekben (8,14) után csökkenti azokat azonos térfogatú test. Így megkapjuk
Súlypontja homogén test gyakran nevezik a súlypontja a hangerőt.
Egyes esetekben a test is feltételezik, egy vékony lemez vagy héj.
Találunk a súlypont a homogén burkolat, feltételezve, hogy a súlya a felületi elem négyzetével arányos az elem
És ezért a test súlya (- részének tekintik a felület).
A meghatározás a súlypont összhangban képletek (8,15), megkapjuk a
A tömegközéppont homogénnek nevezzük burkolat felületi súlypontja.
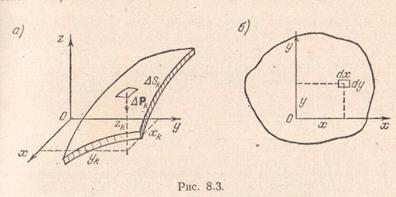
Amint következik képletek (8,16), meghatározzuk a koordinátákat a felületi súlypontja kapcsolódó számítás a integrálok a felület.
Ahhoz, hogy egy lapos egyenletes tányér
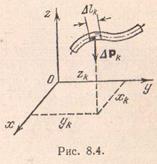
ahol - a hossza a rúd.
Mennyiség az úgynevezett „üldözés súlyát”. A mi feltételezés - állandó. Ezután, összhangban képletek (8,15), a koordinátáit a súlypont homogén rúd formában vannak jelen
Súlypontja a hajlított rúd úgynevezett középvonala gravitáció.