bináris kapcsolatok
Definíció. Bináris reláció R egy részhalmaza pár (a, b) ∈R Descartes-szorzat A × B, R. F. R⊆A × B. A készlet az úgynevezett A domain a kapcsolatok R, a beállított B - az értéktartomány.
Rendeltetése: ARB (.. Azaz, a és b a R reláció). /
Megjegyzés. ha A = B, akkor azt mondjuk, hogy az R egy reláció a halmaz
Módszerek megadásával bináris kapcsolatok
1. lista (párokat), melyek ezt az arányt végezzük.
2. Matrix. Bináris reláció R ∈ A × A., ahol A = (A1. A2. An), megfelel egy négyzetes mátrix a rend n. ahol az elem CIJ. a kereszteződésekben a i-edik sorának és j-edik oszlop egyenlő 1, ha közötti ai és aj az aránya R. helyen, vagy 0, ha nincs jelen:
Legyen R - reláció, R ∈ A × A. Ezután az arány R:
visszaható ha Ɐ a ∈ A: egy R egy (fő diagonális mátrix reflexív reláció tartalmaz csak egység);
tükröződésmentesítő ha Ɐ a ∈ A: egy R egy (fő diagonális mátrix REFLE-intenzitási arányt tartalmaz csak nullát);
szimmetrikusan, ha Ɐ a. b ∈ A: egy R b ⇒ b R egy (mátrix ezen viszony szimmetrikus az fő átlós, azaz CIJ cji);
antiszimmetrikus ha Ɐ a, b ∈ A: a R b b Ra ⇒ a = b (ebben a magatartás mátrixban hiányzó egységek szimmetrikus a fő diagonális);
tranzitívan ha Ɐ a, b, c ∈ A: a R b b R c ⇒ egy R C (ebben a mátrixban kapcsolatot meg kell felelnie: .. ha i-edik sorban egy egységet, például a j-ik koordináta (oszlop) vonalak, azaz CIJ = 1, akkor minden egység J- dik sora (hagyja ezeket egység felel meg k-adik koordinátákat úgy, hogy, CJK = 1) meg kell felelnie a készülék az i-edik sorának az azonos k-adik koordinátákat, t. e. CIK = 1 (és talán még más koordináták).
Célkitűzés 3.1. Határozza meg a tulajdonságait a viszonyított R - «osztóját kell” meghatározni a természetes számok halmaza.
reflexszerűen nélkül tükröződésmentesítő, mivel bármilyen számú osztja magát maradék nélkül: a / A = 1-et minden a∈N;
Ez nem szimmetrikus, antiszimmetrikus, például, 2 elválasztó 4, de nem 4 elválasztó 2;
tranzitívan takkakesli b / a ∈ N és C / b ∈ N, a c / a = b / a ⋅ c / b ∈ N, például, ha a 6/3 = 2∈N és 18/6 = 3∈N, majd 18/3 = 18 / 6⋅6 / 3 = 6∈N.
Célkitűzés 3.2. Határozzuk meg a tulajdonságait R reláció - «hogy egy testvér”, halmazán megadott emberek.
Határozat.
nem reflexív, tükröződésmentesítő miatt nyilvánvaló hiánya ara minden a;
Ez nem szimmetrikus, mint általában egy testvérpár b tart ARB. de nem Bra;
antiszimmetrikus nem, hiszen ha a és b Borrow, majd ARB Melltartó, hanem egy ≠ b;
tranzitív, ha a hívás, hogy az emberek, akik közös szülők (anya és apa).
Célkitűzés 3.3. Határozza meg a tulajdonságait a viszonyított R - «hogy a fő” halmazán megadott szerkezeti elemek
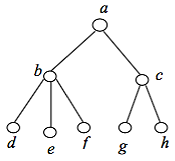
- nem reflexív, tükröződésmentesítő ha egy adott értelmezés nincs értelme;
- Ez nem szimmetrikus, antiszimmetrikus, mert minden a ≠ b nem hajtunk végre ugyanabban az időben, és ARB Bra;
- tranzitív, hiszen ha egy fej a fej a b és b c. a feje egy c.
Feladatok az önálló döntési
Határozzuk meg a tulajdonságait Ri kapcsolat. halmazán megadott Mi mátrix, ha:
Műveletek bináris relációk
Let R1. R1 egy kapcsolat halmazán megadott A.
Opredelenie.Stepenyu kapcsolat R on A halmaz nevezzük annak összetételét önmagával.
Definíció. Ha R ⊂ A × B. akkor R ° R -1 ez az úgynevezett kernel aránya R.
3.1 Tétel. Legyen R ⊂ A × A - kapcsolatban halmazán megadott A.
- R reflexív akkor és csak akkor, ha (a megjelölést használják ⇔), amikor I ⊂ R.
- R szimmetrikusan ⇔ R = R -1.
- R tranzitívan ⇔ R ° R ⊂ R
- R antiszimmetrikus ⇔ R ⌒ -1 ⊂ R I.
- R tükröződésmentesítő ⇔ R ⌒ I = ∅.
Célkitűzés 3.4. Legyen R - közötti arány meghatározza, és az előre meghatározott átviteli párok: R =. Továbbá, S - közötti arány halmazok S =. Számítsuk ki az R -1. S-1 és S º R. Ellenőrizzük, hogy (S ° R) -1 = R -1. S -1.
Célkitűzés 3.5. Legyen R a kapcsolat.” szülő. „És az arány S”. testvér. „A készlet minden ember. Adj egy rövid szóbeli kapcsolat leírása:
R -1. S -1. R ° S, S -1 ° R 1 és R º R.
R -1 - arány”. gyermek. „
S -1 - arány”. testvér. „
R ° S - arány”. szülő. „
S -1 ° R -1 - arány”. gyermek. "
R ° R - arány”. nagymama vagy nagypapa. "
Feladatok az önálló döntési
1) Legyen R - arány”. apja. „S - arány”. nővére. „A készlet minden ember. Adj egy verbális kapcsolat leírása:
R -1. S -1. R ° S, S -1 ° K -1. R º R.
2) Legyen R - arány”. testvér. „S - arány”. anyja. „A készlet minden ember. Adj egy verbális kapcsolat leírása:
R -1. S -1. S ° R, R -1 ° S -1. S º S.
3) Legyen R - arány”. nagyapa. „S - arány”. fia. „A készlet minden ember. Adj egy verbális kapcsolat leírása:
R -1. S -1. R ° S, S -1 ° K -1. S º S.
4) Legyen R - arány”. lánya. „S - arány”. nagymama. „Mnozhe- stve minden ember számára. Adj egy verbális kapcsolat leírása:
R -1. S -1. S ° R, R -1 ° S -1. R º R.
5) Legyen R - arány”. unokahúga. „S - arány”. apja. „A készlet minden ember. Adj egy verbális kapcsolat leírása:
R -1. S -1. S ° R, R -1 ° S -1. R º R.
6) Legyen R - aránya „testvér. „És S - aránya” anya. „A készlet minden ember. Adj egy verbális kapcsolat leírása:
R -1. S -1. R ° S, S -1 ° K -1. S º S.
7) Legyen R - arány”. anyja. „S - arány”. nővére. „Mnozhe- stve minden ember számára. Adj egy verbális kapcsolat leírása:
R -1. S1, R ° S, S1 ° R1, S º S.
8) Legyen R - arány”. fia. „S - arány”. nagyapa. „A készlet minden ember. Adj egy verbális kapcsolat leírása:
R -1. S -1. S ° R, R -1 ° S -1. R º R.
9) Legyen R - hozzáállás”. nővére. „S - arány”. apja. „Mnozhe- stve minden ember számára. Adj egy verbális kapcsolat leírása:
R -1. S -1. R ° S, S -1 ° K -1. S º S.
10) Legyen R - arány”. anyja. „S - arány”. testvér. „A készlet minden ember. Adj egy verbális kapcsolat leírása:
R -1. S -1. S ° R, R -1 ° S -1. R º R.