Az elméleti feladatok komplex változó
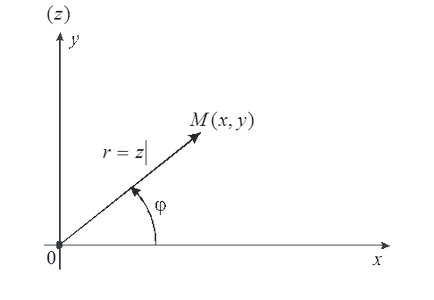
A bezárt szög a valós tengelynek Ox és a vektort nevezzük argumentum egy komplex szám z. . Érték zárt rés, az úgynevezett legfőbb értéke az argumentum (kijelölési -Arg z):
A fő értéke az érvelés egy komplex szám Z lehet meghatározni a általános képletű
Definíció. rekord típus
Ez az úgynevezett trigonometrikus forma egy komplex szám z.
Megjegyzés. Egy komplex szám Z is rögzítik exponenciális formában
Összehasonlításképpen, komplex számok, és csak az egyenlőség művelet kerül bevezetésre: a komplex szám egyenlő, és ha igen, illetve a valós és a képzetes rész :. Az egyenlő számban írt trigonometrikus formában van, az alábbiak szerint történik: ha a modulok vannak egyenlők, és az érvek kapcsolódó
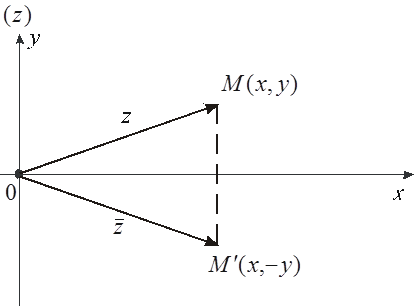
Definíció. Két komplex számok úgynevezett komplex konjugált számokat. Ehhez használja a kijelölése és (2. ábra).
16.1.2. vonatkozó összeadás, kivonás, szorzás és osztás.
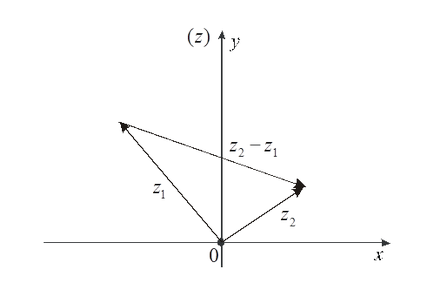
-, hogy két komplex számok (például), akkor meg kell határozni azokat külön-külön a valós és képzetes része, amelyet a valós és képzetes része a számok összege. Képletek (1.7) és (1.8) találunk
A terméket a komplex számok és (jelezzük) kifejezés egy komplex szám z. egyenlő
Amatőr komplex számok és ez határozza meg a működését szorzás és lehet tenni az alábbi képlet szerint
Gyakorlati jogszabály másképp. Mivel a formula (1.10) célszerű elvégezni a Division a következőképpen:
Mivel ezek a műveletek összeadás és a szorzás a komplex számok vannak kitéve ismert öt aritmetika törvényeit:
1. (kommutativitás);
2. (asszociativitás kívül);
3. (kommutativitás többszörözés);
4. (asszociativitás szorzás);
5. (disztributivitás szorzás tekintetében
Képlet (1,10), „felfedi a jelentése” a képzeletbeli egység. " Így, a szorzás a komplex számok végzi szokásos szabályait algebra a cserélendő -1.
Itt a megoldás „tipikus példák” fogalmak fent bevezetett.