Számszerű adatokat a feladat № 4 - studopediya
5. 2. Rövid útmutató és egy példát a probléma megoldásának
Mielőtt a problémamegoldás, fel kell tárnia a témája a „súlypontja”. Megköveteli erősen fogja meg a koncepció statikus pillanat, tudni, hogy a helyzet a súlypontok egyszerű geometriai formák és meg tudja határozni a koordinátákat a súlypontok a bonyolult keresztmetszetek képviselő egy sor egyszerű geometriai formák és keresztmetszetek kialakított szabványos hengerelt profilok (az utóbbi esetben meg kell, hogy képes legyen használni az asztalok GOST). A következő terv segítségével oldja meg a problémát:
- split szakaszt egyszerű formák. Ezek a számok a standard hengerelt profilok amelynek méreteit az 1. mellékletben megadott;
- adja meg a súlypontokat az egyes profilok (ábra) és jelzésére C1. C2. ..., Cn;
- válasszon egy rendszer koordinátatengelyek X, Y;
- A képlet, hogy meghatározzuk a koordinátákat a súlypont a keresztmetszet, hogy meghatározzuk a koordinátákat a pont;
- pozícióját mutatják a súlypont az ábrán (a C pont), és azt mutatják, a távolság a súlypont és a koordináta tengelyek;
- helyességének ellenőrzésére a döntés lehet változtatni a helyzetét koordinátatengelyeken (vagy az egyik tengely), és megtalálni a koordinátákat a súlypont képest új tengelyt. A tömegközéppont nem attól függ, hogy a rendszer a kiválasztott koordináta-tengely.
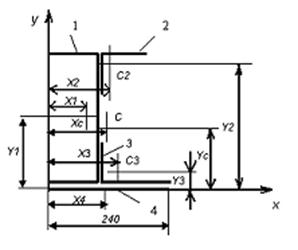
Határozza meg a koordinátáit a tömegközéppontja a keresztmetszet (4.1 ábra ..) Alkotják: 1 - párkány №30; 2 - azonos szögben 12 100 100; 3 - egyenlőtlen sarok 140 90 10; 4 - keresztmetszete az acéllemez 240 10 mm-es. ___________________________
1. A mix távozik a táblázat (1. függelék) szabvány hengerelt profilok eléréséhez szükséges az alábbi feladatokat:
A párkány № 30 (. Ábra 4. 2.) - h = 300 mm = 30 cm; b = 100 mm = 10 cm; Z0 = 2,52 cm; A = keresztmetszeti területe 40,5 cm 2.
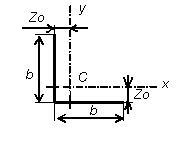
Az egyenlő szögek 12 100 100 (.. 4.3 ábra) - b = 100 mm; Z0 = 2,91 cm; A = 22,8 cm 2.
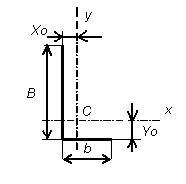
Egyenlőtlen sarok 140 90 10 (.. 4.4 ábra) - B = 140 mm; b = 90 mm; x0 = 2,12 cm; y0 = 4,58 cm; A = 22,2 cm 2.
A acéllemez A = 24 cm2.
2. A választás a kiegészítő rendszer koordinátarendszer megtalálják a relatív koordinátáit annak súlypontja az egyes elemek:
koordinálja a súlypont C1 párkány szakasz:
koordinálja a súlypont a C2-szakasz egyenlő szögek:
koordinálja a tömegközéppontja a keresztmetszet C3 egyenlőtlen sarok:
Koordinátái súlypontja a keresztmetszet az acéllemez C4:
A koordináták a súlypontok az összes elem pozitív, mert az összes kijelölt szakasz tekintetében a koordinátatengelyek található, az első negyedben (az első negyed).
3. Határozza meg a koordinátákat a súlypontja minden keresztmetszetek:
A létrejövő koordináták xc és yc fel vonópontra C.
Tesztelje tudását
1. Mi az úgynevezett súlypontja a test?
2. Írja a képlet meghatározására a koordinátáit a súlypontok a test egységes és homogén vékony lemez.
3. Milyen a helyzet a súlypontok egyszerű geometriai alakzatok?
4. Milyen az súlyponthelyzet síkidom komplex alakja?
5. Hogyan súlypontjának a keresztmetszet áll szabványos hengerelt profilok?