Segítségével integrálok megtalálásához térfogatának forgástest, tartalom platform
Tanár középiskolai №12
Segítségével integrálok megtalálásához térfogatának forgástestek
A gyakorlati hasznosságát matematika annak a ténynek köszönhető, hogy nem
speciális matematikai ismeretek nehéz megértés eszköz elvek és a modern technológia. Minden ember az életedben teljesítenie meglehetősen összetett számításokat, használja a köznyelv technikát, hogy megtalálják a könyvtárak használatához szükséges formula, hogy egyszerű algoritmusok problémák megoldására. A modern társadalomban egyre több szakma igénylő magas szintű oktatást, mivel a közvetlen alkalmazása a matematika. Így egy diák matematika válik jelentős szakmai téma. A vezető szerepe van a matematika kialakulását algoritmikus gondolkodás, elősegíti a cselekvőképességét algoritmus szerint és a design új algoritmusok.
A tanuló a kérelemmel érintett az integrál kiszámításához térfogat forgástestek, azt javaslom, hogy a diákok tanórán kívüli tevékenységek, hogy fontolja meg a témát: „A kötet a forgástestek és integrálok.” A következő idézet iránymutatások a figyelmet a téma:
1.Ploschad síkidom.
Algebrai Persze tudjuk, hogy a fogalom a határozott integrál eredményezett gyakorlati feladatokat. Egyikük, a számítási területének síkidom határolt egy folyamatos vonal y = f (x) (ahol f (x) 0) és az egyenes vonalak x = a és x = b, és a vízszintes tengelyen; ez a szám lesz az úgynevezett görbe vonalú trapéz.
Kiszámoljuk a területet a görbe vonalú trapéz formula, ha a trapéz alapja fekszik az x tengelyen, vagy a képlet, ha trapéz bázis rejlik az ordinátán.
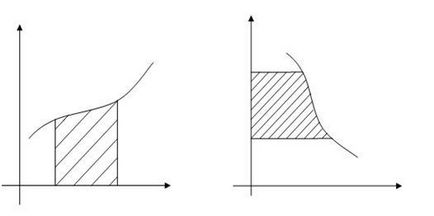
2.Obem forgástest.
Forgástest a legegyszerűbb esetben: olyan szerv, amely merőleges síkokban egy egyenes vonal (forgástengely) mentén metszik körök középpontja ezen a vonalon. Képletek kiszámításához a hangerőt a forgástest. A keresztmetszet a test által merőleges síkban az Ox tengely egy kör, amelynek területén.
Ahhoz, hogy megtalálja térfogata forgástest kialakított forgatásával trapéz ívelt a tengely körül Ox, korlátos folytonos vonal y = f (x), a tengely Ox, egyenes vonalak x = a és x = b képlettel számítottuk ki
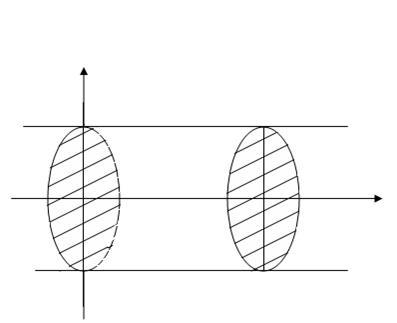
Mivel a vonalszakasz BC fekszik y = R (R - a sugara a bázis a henger), a hangerőt egy ilyen henger lelet képlet. Legyen a = 0, b = H (H - magassága a henger), majd a.
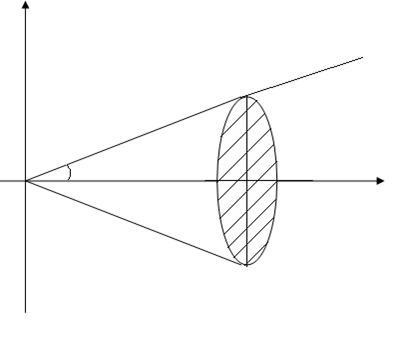
Szegmens AB fekszik a vonalon y = kx + c, ahol c = 0, mert a vonal áthalad a ponton (0, 0). Így közvetlen kilátás.
Legyen a = 0, b = H (H a magassága a kúp), akkor V
5.Obem csonka kúp alakú.
A csonka kúp nyerhető forgatásával a téglalap alakú trapéz ABCD (CD Ox) a tengely körül Ox.
Szegmens AB fekszik a vonalon y = kx + c, ahol. c = r.
Mivel a vonal áthalad a pont (0; r).
Így közvetlen kilátás.
Legyen a = 0, b = H (H a magassága egy csonka kúp), majd a
A labda lehet beszerezni forgatásával a kör középpontja (0, 0) a tengely körül Ox. Félkör felett található a tengely Ox, adják
Ezért, a térfogata a gömb által meghatározott képlettel
7.Obem gömbszelet.
Gömbölyű az a része, egy gömb, sík cut-off is.
Használata képletű találni kötet egy gömb térfogatát a szegmens a következő képlet szerint.
Ebben az esetben a = R-H, b = R (H - magassága a szegmens, R - a gömb sugarának). Ezért van, hogy a
Ugyanígy találunk V
Ez a megközelítés hozzájárul a kreativitás fejlesztését és a logikus gondolkodás, lehetővé teszi, hogy pótolja a tudásmennyiség diákok, hozzájárul a minőségi oktatás. Ezt a módszert már tesztelték az általam a 11. évfolyamon. Ő adott pozitív eredményt.