sűrűségfüggvénye (PVR) - studopediya
Annak a valószínűsége, dP, hogy egy folytonos valószínűségi változó lesz az értéke tartozó intervallum (x. X + dx) egyenlő
,
ahol f (x) - a sűrűségfüggvénye (a valószínűsége egységnyi hossza a figyelembe vett szakasz).
Annak a valószínűsége, hogy a valószínűségi változó veszi értékeket intervallumban [x1, x2] kiszámítása a képlet:
f (x) függvény az alábbi fontos információkat: egy x számszerű értékkei a valószínűsége, hogy egy nagyobb értékre száma x1 és x2 kisebb, mint a görbe alatti terület f (x), az [x1. x2]. Természetesen ez vonatkozik minden x1 és x2. szorosan kapcsolódó vagy távoli bárhol a sorban x.
Között a legismertebb fajta eloszlás folytonos valószínűségi változók leggyakrabban használja a normális eloszlás által leírt Gauss törvénye. Ez az első alkalom a szokásos gyakorlat találtak H1H században alkalmazott mérési hiba az elmélet a Laplace és Gauss.

Gauss (Gauss) Karl Fridrih (1777/04/30, Braunschweig, - 1855/02/23, Göttingen), német matematikus, aki alapvetően hozzájárul a csillagászat és geodéziai

Most, miután a bevált AM Lyapupovym a központi határeloszlás tétel. Világossá vált, hogy miért a rendes törvény széles körben elterjedt a mérnöki, a biológia, a szociológia, a pszichológia és sok más területen az emberi tudás.

Ljapunov Aleksandr Mihaylovich [25,5 (6,6). 1857 Jaroszlavl - 1918/11/03, Odessza], magyar matematikus és mérnök, akadémikus az Petersburg Tudományos Akadémia.
A centrális határeloszlás-tétel kimondja, hogy ha egy véletlen érték generálódik hozzáadásával nagyszámú független valószínűségi változók véges eltéréseket, a törvény terjesztése a véletlen változó gyakorlatilag normális törvény. Mivel a véletlen változók mindig létrehoz egy végtelen számú oka, és gyakran egyikük sem rendelkezik variancia, amely összehasonlítható a varianciája véletlen változó, a többség a gyakorlatban felmerült véletlen változók engedelmeskedik normális eloszlás törvény.
Például a magassága egy ember, ami számos tényező befolyásolja, melyek közül a tömege nem domináns befolyását.
A normális eloszlás, más néven Gauss-eloszlás vagy Gauss-eloszlás - egy valószínűségi eloszlás, amelyet meghatározott sűrűségfüggvénye:
ahol a paraméter # 956; - az átlagos érték (elvárás) egy véletlenszerű változó, és jelzi a koordináta a maximális eloszlási sűrűsége görbe, és a # 963; ² - diszperzió.
A sűrűségfüggvény a normál joggal,
1.2 - grafikonok egy középső # 956; és a különböző szórások # 963;. és
A grafikon a valószínűségi sűrűsége a normális eloszlás törvény szimmetrikus a függőleges vonal X max = # 956;. És azon a ponton,
X max = # 956; funkció maximum egyenlő.
Továbbá, a terület alatt a teljes görbe f (x) jelentése 1, azaz a a valószínűsége, x, hogy a vonal értéke 1, és ez egy jelentős esemény. Ez a tulajdonság is nevezik a normalizációs feltételt.
változó # 956;. El tud végezni párhuzamos eltolása a görbe f (x) az x tengely mentén. Az is látható, hogy a legvalószínűbb előfordulási x A kísérletben közel # 956;. alatti terület f (x) bármely intervallumban, amely tartalmaz # 956;. a legnagyobb.
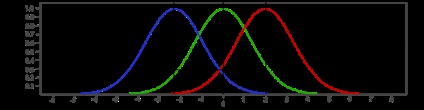
szám # 963; az átlagos eltérés a numerikus index száma x # 956;, a kevésbé # 963; a „hűvösebb” lesz a „hegy” f (x), és annál kevésbé valószínű, hogy nagyon különbözik x μ.
Éppen ellenkezőleg, a nagy # 963; „Hill” f (x) terjed át a „sima” és szinte azonos valószínűséggel, úgy tűnhet, mint egy közeli # 956;, és önkényesen messze # 956; .
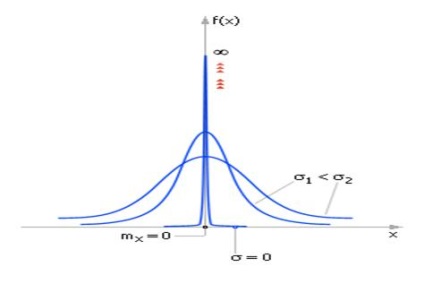
Annak a valószínűsége, hogy egy valószínűségi változó eltér a matematikai elvárás nagyobb mennyiségben, mint háromszorosa a szórás gyakorlatilag nulla.
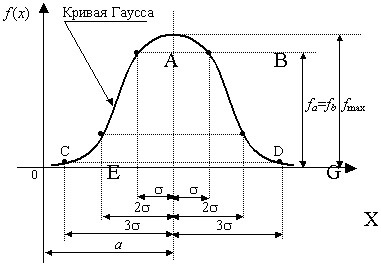
A számítások azt mutatják, hogy a valószínűsége, hogy egy normális eloszlású valószínűségi változó a tartományban a következőket:
I. P (μ- # 963; II. P (μ-2 # 963; III. P (μ-3 # 963; A gyakorlatban úgy gondoljuk, hogy ha valamilyen - bármilyen véletlen változó el három szigma szabály szerint ez a véletlen változó normális eloszlású. Gauss-eloszlás - az egyik leggyakoribb a fizikában. Egy ilyen terjesztésüket mérési hibák fizikai mennyiségek, az eredmények a céllövészet, a forgalmazás, a nyúlványok gázmolekulák sebességgel (Maxwell eloszlás), a valószínűsége kis ingadozások, és így tovább.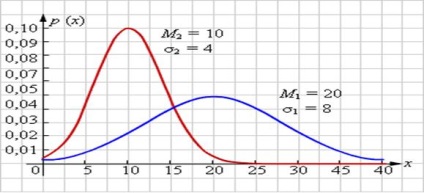
Kapcsolódó cikkek