Pendulum - fizika (mechanikai rezgések és hullámok)
Tekintsünk egy egyszerű inga - a labda felfüggesztett egy hosszú erős cérnát. Egy ilyen inga az úgynevezett fizikai. Ha a méret a labda sokkal kisebb, mint a hossza a menet, majd ezeket a méreteket lehet elhanyagolni, és tekinthető anyagi pont labdát. Stretch fonal is lehet figyelmen kívül hagyni, mert nagyon kicsi. Ha a fonal tömegének sokszor kisebb, mint a tömeg a labdát, a súlya a fonal is lehet figyelmen kívül hagyni. Ebben az esetben van egy modellt az inga, amely egy matematikai inga.
Ez az úgynevezett matematikai inga anyagi pont tömegű m m. függesztve a súlytalan nyújthatatlan fonalat L hossza L a gravitációs tér (vagy más erők).
Galileo Galiley kísérletileg úgy találta, hogy a matematikai inga oszcilláció időszakban egy olyan területen a gravitáció nem függ a tömegét, és a rezgés amplitúdója (a szög a kezdeti alakváltozás). Azt is megállapították, hogy a rezgési periódus egyenesen arányos az L - - √ L.
Időszak kis matematikai inga oszcilláció a Föld gravitációja határozza meg Huygens:
T = 2 π L g - - √. T = 2 π L g.
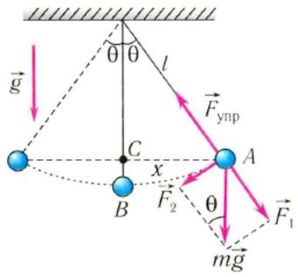
Matematikailag inga eltérítési szöge α <20 0 α <20 0 погрешность расчета периода по формуле Гюйгенса не превышает 1 % 1 %.
Általában, amikor az inga homogén területeken több erő kell lépnie a „tényleges gyorsulás» g * g * meghatározni a rezgési periódus. jellemző a kapott hatásait ezeken a területeken, és az átmeneti időszak oszcilláció az inga fogja meghatározni a következő képlettel
T = 2 π L g * - - - √. T = 2 π L g *.