Példák a hányadost és a nucleus (geometrikus) magasabb algebra
Próbáld ki, mivel az üzemeltető, hogy a vetítés. Például, egy párhuzamos síkban egy vektorba. Még csak egy vetülete egy síkban a tengellyel párhuzamos.
Még mindig nem értem, ha a hányados, és ahol a kernel. Adjon meg példákat és jelezze, hol van egy hányados tér és a kernel. Ez sem jöhet hozzám, akkor.
Ne.
Adj magadnak néhány példát lineáris funkcionálok a geometria, és mi segítünk a magja (és azokat a szörnyű hányadosa)
Euklideszi normája háromdimenziós vektorok.
Itt olvastam a Kolmogorov (és több tucat más könyvek). Itt van egy kis vágás.
Hagyja, hogy a lineáris tér és némi altér. Két elem és az egyenértékű, ha a különbség tartozik. Ez az arány osztja minden osztályban. Az azonossági osztály elemei az úgynevezett mellékosztály (a altér). A gyűjtemény minden ilyen osztályok hívják hányadosa helyet az altér.
Azt hiszem.
Példaként a háromdimenziós altér idézhetjük: a gépet, a szegmensek már nem jut eszembe (lehet, hogy több példát). Itt van festve, mint a különbség egyetlen pár vektorok és a különbség a másik pár a vektorok fekszenek ugyanabban a síkban (ami egy altér trehmerki):
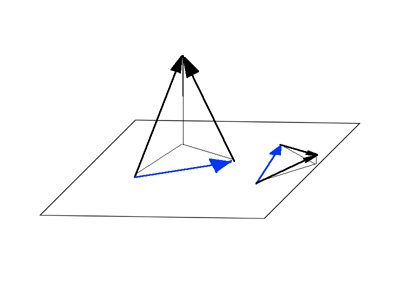
Van egy vektor, amely a különbség a másik síkon. az osztály vektorok minden síkon, a különbség, amely abban rejlik benne. Akkor nem értem, ha a hányados helyet itt.
Most a funkcionális (kihagyja „lineáris” a rövidség kedvéért).
Felhívjuk a sor kernel tetszőleges sor a pont, hogy van egy szám minden, hogy mikor. Domború, amelynek a magja nem üres, az úgynevezett egy konvex testet. A háromdimenziós euklideszi térben, egy kocka, gömb, tetraéder konvex test.
Például egy kocka háromdimenziós térben, -Három dimenziós térben -A kocka. - az általános esetben, a lényeg a háromdimenziós térben, amely nem szükséges, hogy a belsejében vagy határán a kocka, de lehet azon kívül is. Mi ez, nem tudom elképzelni.
Szegmens - nem éppen egy altér. És a gép - nem minden.
Egyenesen a lényegre. A összege két vektor a sorban fog feküdni egy egyenes vonal, skálázott vektor emellett fekszenek egy egyenes vonal. Ugyanez a síkon. Ha ez nem altér, akkor megszegik a 8. tulajdonságai összeadás és a szorzás egy skalár?
Geometriailag kényelmes feltételezni, hogy a vektorokat ábrázolni egy fix pont. Aztán végük leírni néhány részhalmaza pont. Melyik felel meg egy részhalmaza altér?
Az átmenő síkban fix pont?
a mag egy ilyen funkcionális (vetítés) - vektorok ortogonális tengelyek,
Természetesen. Ie volt. síkra.
És ha a kocka - a kernel, nem érti?