Moment erő a lényeg, és a tengely, a klasszikus mechanika
Pillanata erő a körül a pont O - egy vektor, amelynek modulusa egyenlő a termék a hűtőbordák a vállon - a legrövidebb távolság O pont a erővonal. Az irány a perdület vektor merőleges erő a áthaladó sík pont és a hatóirányának erő, hogy keresi az irányt a perdület vektor, forgatás, által elkövetett erő pont körül O, az óramutató járásával megegyező.
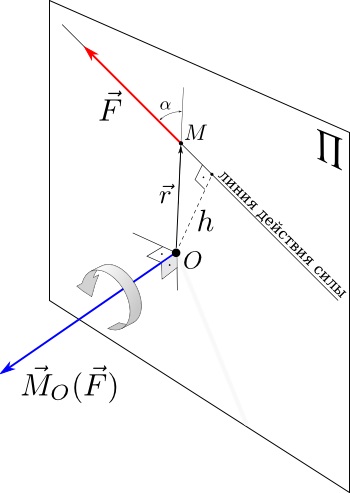
Ha tudja, hogy a sugár vektor $ \ vec R $ pontján az erő alkalmazása $ \ vec F $ képest az O pont az a pillanat, ennek az erőnek a O a következőképpen fejezhető ki:
$$
\ Vec M_O (\ VEC F) = \ vec r \ alkalommal \ vec F.
$$
Valóban, a modul a vektor termék:
$$
| \ Vec M_O | = | \ Vec r \ times \ vec F | = | \ R Vec | | \ Vec F | \ Sin \ alpha.
$$
Összhangban a szám $ | \ vec r | \ sin \ alpha = h $, így:
$$
| \ Vec M_O | = | \ Vec F | h.
$$
Vector $ \ VEC M_O $, ennek eredményeként a vektor termék merőleges vektorok $ \ r VEC $ és $ \ VEC F $, $ sík tartozó \ Pi $. Az irányt a vektor $ \ vec M_O $ olyan, hogy keresi az irányt a vektor, a legrövidebb forgási $ \ r VEC $ és $ \ vec F $ az óramutató járásával megegyező. Más szavakkal, a vektor $ \ vec M_O $ teljessé a rendszert vektorok $ (\ r VEC, \ VEC F) $ jobbra három.
Ismerve a pont koordinátáit az az erő alkalmazása egy koordináta-rendszerben, amelynek eredete egybeesik az O pont, és a nyúlvány a erők a koordináta tengelyen, a pillanatnyi erőt lehet meghatározása a következő:$$
\ Vec M_O = \ vec r \ times \ vec F =
\ begin
\ Vec i \ Vec j \ Vec k \\
x y z \\
F_x F_y F_z
\ End = (y F_z - z F_y) \ vec i + (Z F_x-x F_z) \ vec j + (x F_y-y F_x) \ vec k.
$$
Pillanata erő tengely körüli
A vetítés a pillanatban az erő egy adott pontot egy átmenő tengely ezen a ponton az úgynevezett pillanatok erő a tengely körül.
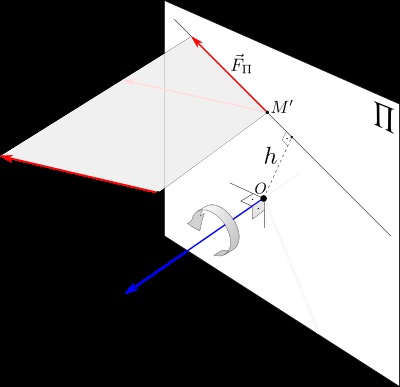
Pillanatában hatályos tengelyhez képest a számítjuk idején vetülete az erő $ \ vec F $ a gépen $ \ Pi $, tengelyére merőleges, tengelyéhez viszonyítva metszéspontja a repülőgép $ \ Pi $:
$$
M_z (\ VEC F) = M_z (\ vec F_ \ Pi) = \ pm F_ \ Pi h.
$$
pillanatban a jel által meghatározott forgásirány, amely hajlamos, így a test erejét $ \ VEC F_ \ Pi $. Ha megvizsgáljuk a tengely irányában a Oz $ $ erő forgatja a testet az óramutató járásával megegyező pillanatban veszik a jel `` plusz „”, vagy - `` negatív „”.