Milyen mozgás síkja párhuzamos eltolás, forgatás,

Ha az egyes pontok a síkban van rendelve egy pont ugyanabban a síkban, és ha bármely pontján ebben a síkban van leképezve egy bizonyos ponton, akkor azt mondjuk, hogy ez a leképezés a repülőgép-ra is. Bármilyen feltérképezésével síkra, amelyben állandó marad pontok közötti távolság az úgynevezett mozgás síkjára.

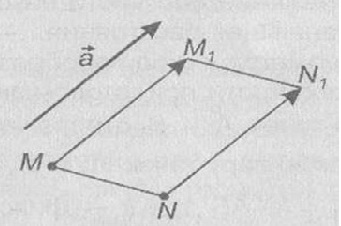
Párhuzamos transzfer. Legyen egy - ez vektor. Párhuzamos fordítás vektort nevezzük a feltérképezése a sík, amelyben minden pont M, hogy a pont M1 jelenik meg. MM1 vektort, amely vektor.

Párhuzamos átadása a mozgás, mint a feltérképezése a síkot, amelyen megőrzi távolságok. Szemléletesen, ez a mozgás lehet képviseli, mint egy elmozdulás a teljes sík irányában a vektor és a hossza.

Forduljon. Jelöljük a sík O pont (forgási középpont), és szöget zárnak α (forgásszög). Forgatás a síkban körülbelül az O pont szögben α nevezzük a feltérképezése a sík, amelyben minden pont M, hogy a pont M1 jelenik meg. hogy OM = OM1 és MOM1 szög egyenlő az alfa. Ebben az esetben az O pont a helyén marad, amely megjelenik a maga és az összes többi pont körül forgatják az O pont ugyanabban az irányban - .. órajárással megegyező vagy ellentétes (az ábra bemutatja az óramutató járásával ellentétes forgás).

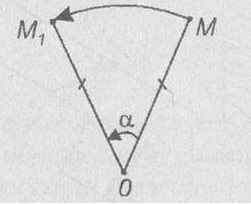
Forgatás egy mozgás, mint a kijelző sík, amelyben a tárolt távolságokat.

Geometriai transzformáció sík, amelyben minden egyes pár A és B pontok jelenik meg egy pár A1 és B1. hogy A1 B1 = k ∙ AB, ahol k - rögzített erre a konverzió egy pozitív konstans úgynevezett hasonlósági transzformáció. A k hívják a hasonlósági koefficiens.

Nyilvánvaló, hogy a repülőgép mozgása - saját hasonlóság esetén (a tényező 1).

Ábra F, úgynevezett egy ilyen alak F. Ha van egy hasonlósági transzformáció, amelyben egy alak F ábra mutatja az F1. Így ezek a számok különböznek csak a méret, forma F és F1 azonos alakzatokat.

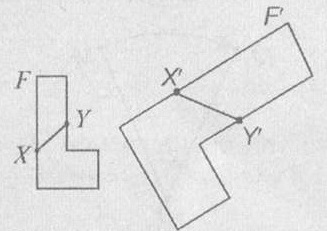
Tulajdonságok hasonlósági transzformáció.

1. A hasonlósági transzformáció megőrzi a kapcsolat szegmensek párok: ha az AB és CD - két tetszőleges hosszúságú, és az A1 és B1 C1 D1 - a képek, az A1 B1 / C1 D1 = AB / CD.
2. Egyenlő szegmensek jelennek egyenlő; középpont - a közepén a kép.
3. Ha meghatározott síkban két derékszögű koordináta-rendszer, és mivel a k> 0. Ekkor egyedileg meghatározott hasonlósági transzformáció egy k együtthatót, amely megjeleníti a tengelye az első koordinátarendszer az azonos második tengely.

Geometriai transzformáció síkban egy fix pont S, amelyben minden pont, eltér S, rendel egy pont A1. hogy SA1 = k ∙ SA, ahol k ≠ 0 - előre kijelölt számot, úgynevezett homothety középpontú S k, és egy együttható. Ha F1 ábra származik az ábrán F segítségével kitágulása, az ábrán az F és F1 nevezzük homothetic.

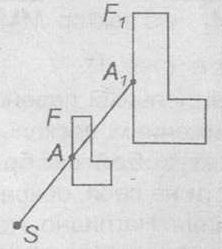
1. Homothety a K együttható a hasonlóság │k│ tényező.
2. Dil vesz minden egyenes párhuzamos vele vonalat.
3. Bármilyen homothety lehet állítani homothetic központ és egy pár kölcsönösen megfelelő pontokat.