Mi - mező - matematika
A „mező” képzést egy folyamán magasabb algebra.
Adunk pontosabb meghatározását.
Field egy nem üres halmaz P, amelyen két bináris algebrai művelet van definiálva, az úgynevezett összeadás és szorzás, 10 megfelelnek a következő axiómák:
1.A minden a, b, c, tartozó P, (a + b) + c = a + (b + c) - asszociativitása mellett;
2. Minden olyan a, b tartozó P, a + b = b + a - kommutativitás;
3. Van egy nulla elemet 0 tartozó P, hogy minden elem a tulajdonában lévő P, a következő egyenlőség: 0 + a = a + 0 = a - megléte nulla elemet;
4. bármely elem egy munkát létezik, hogy a következő egyenlőség: A + (- a) = (- a) + a = 0 - a létezését az egyes ellentétes elem;
5. Bármely a, b, c, tartozó P, (a + b) * c = a * c + b * c, a * (b + c) = a * b + a * c - disztributivitás szorzás felett mellett;
6. Bármely a, b, c, tartozó P, (a * b) * c = a * (b * c) - asszociatív szorzás;
7. minden a, b tartozó P, a * b = b * egy - a szorzás kommutatív;
8.Suschestvuet identitás elem 1. tartozó P, amely bármely elem a tulajdonában lévő P, az egyenlőség: 1 * a = a * 1 = a - létezése egyetlen elem;
9.0 nem egyenlő 1-gyel 0,1 P tartoznak;
10.Dlya bármely elem egy, nem egyenlő nullával, van egy inverz 1 / a (mínusz az első fokú) úgy, hogy az egyenlet: a * 1 / a = 1 / a * a = 1 - létezése egy inverz elemre minden nem nulla.
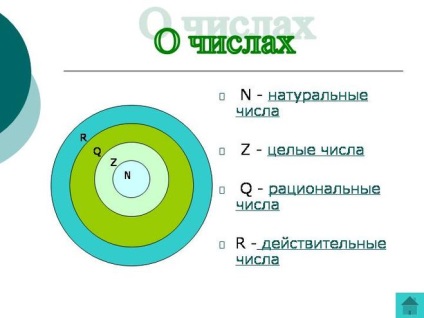
A számsorral, amelyeket tanult az iskolában (lásd a képen), a mező csak példák a racionális és valós számok, hiszen minden körülmények között a mező meghatározása. A természetes számok halmaza (1,2,3). És egész számokat (. -3, -2, -1,0,1,2,3,4.) Nem képeznek egy olyan területen, mint a természetes számok nem az axiómák 3 , 4,9,10 (elég, még nem teljesítése egy axióma 3, akkor nem lehet ellenőrizni), és egész - axióma 10.
A matematika területén használják kétféleképpen.
Először is, a mező - egy sor tárgyak, amelyek esetében a vonatkozó összeadás, szorzás és osztás (kivéve a nullával való osztást objektum), az ilyen tárgyak, az eredményeket ezek a műveletek a beállított. Emiatt a mező egész számok nincsenek: művelet eredményét „1 osztva 2”, nyilván, az egész számok nem tartoznak. Ez állítja egy osztály az úgynevezett „gyűrű”.
De a racionális számok egy területen már: elosztjuk egy számot egy másik ésszerű gazdálkodás továbbra is racionális szám.
Másodszor, a területen - van. ezen a területen. Mi hívtuk területén a fizikai szempontból. Kellő általánosság feltehetjük, hogy a területen - egy olyan funkció, számos változó: ha rendelni egy szabályt, mely szerint minden egyes pontja M hozzárendelünk egy értéket a K (nem feltétlenül páros - ez lehet a vektor mind az elektromos térerősség, és még tenzor, mint az általános relativitáselmélet), akkor van így a térben, amely tartozik a M pont, mivel a területen.
Legyen - sokat.
Definíció: A - mező. ha A - kommutatív gyűrű 1 (a egység), amelyben, minden x ≠ 0 léteznek H ---- ¹ - visszatérés tagja, oly módon, hogy: x · h ---- ---- ¹ = X- ˉ ------ ---- ---- ¹ · x = 1 ---
Most mi kell érteni, hogy egy ilyen gyűrű kommutatív gyűrű és gyűrű 1.
Def. A - az A gyűrű. Ha két művelet van definiálva az A:
- Minden x, y A --- → x + y A - mellett;
- Minden x, y --- → tól x · y az A - szorzás;
úgy, hogy a következő axiómák:
- x + y = y + x;
- x + (y + z) = (x + y) + z;
- Van egy 0 (nulla elemet) úgy, hogy x + 0 = 0 + x = x;
- Minden x létezik (-x) úgy, hogy a (-x) + x = 0;
- x (yz) = (xy) z;
- x (y + z) = xy + xz;
Def. A - ha az A gyűrű 1 - gyűrű és van egy 1 (egységeleme) úgy, hogy x = 1, · · x 1 = x.
Köszönjük! És hogyan használják? Tudna egy példát egy kis barátságos? - 3 éve
Nos, például, hogy az egész számok Z. Lássuk, ez lesz a területen, vagy nem? A hipotézis, ha Z - mező, meg kell gyűrű kommutatív gyűrű és a gyűrű 1, és így az inverz bármely elem Z.
Élvezi ..
A Z-gyűrű?
Igen. Szorzás, kívül jelen. Minden axiómák teljesülnek.
Van Z kommutatív gyűrű?
Így is, úgy is. Például, 5 * 3 = 3 * 5 = 15
A Z 1 gyűrűs?
Igen, ez az.
DE Z nem olyan területen, mert nincs inverz elem minden eleme Z, így egészek. A fordított cell - van 1 osztva ezt a nagyon eleme. Például egy 3 és 1/3. És a harmadik - ez nem egy egész szám.
De több irracionális számok (Q) és az anyag (R) lesz mezőket. Kiválogattam most? - 3 éve
Úgy van beállítva, amely az összes számot egy bizonyos tulajdonság. Például, a mező egész számok.
Ismeretes, hogy a műveletek a összeadás, kivonás és szorzás felett végzett területén egész számok.
Ez azt jelenti, hogy ha összeadás, kivonás, vagy két számot, akkor kap egy egész szám.
A részleg - nem meghatározott. Előfordul, hogy elosztjuk az egyik egység egy másik egység, megkapjuk a racionális.
Ezért mind a négy aritmetikai műveleteket végeznek át a racionális számokat.
Nem számít, hogyan összeadni, kivonni, szorozni és osztani a racionális számok, megint kapunk racionális.
Sad Roger [170K]
Egész számok nem alkotnak területeken. Ők alkotják a másik osztály szettek - gyűrűt. - 3 éve
Igen, talán. Nem vagyok jó a térelméletet matematika.
De valójában én még mindig jobb. Field - egy számsor, amely bizonyos tulajdonság. - 3 éve