metszéspontjában
Legyen adott egy tetszőleges halmaz A és B
Definíció: A metszéspontja az A és B az A halmaz

A



Fontolja meg a készlet A és B ábra mutatja a kereszteződés ezen halmazok. Legyen:
1) A és B halmaz nem kerülnek kapcsolatban egymással.
Nyilvánvaló, hogy ebben az esetben egy

2) meghatározza az A és B viszonyában az egyenlőség.
Ekkor A

3) az A és B van a felvétel.
Ha egy




Kikelés mutatja elemek sokaságát tartozó

4) az A és B viszonylatában kereszteződés.

Dupla kelési mutatja elemek sokaságát tartozó

Legyen A = a; b>, B =. találunk egy

Meghatározzuk a kereszteződésekben a két A


Megjegyzés: A beszéd, hogy a művelet kereszteződés megfelel az „és”. és egyesíti műveletek - a „vagy”.
Így, definíció szerint, x





A metszéspontja az A és B nem ezek az elemek nem a A. vagy B. Így, X





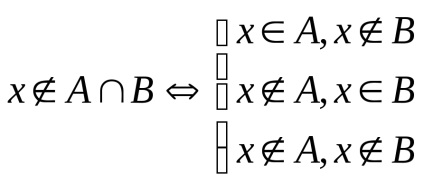
Megjegyzés. A művelet a megállapítás a szövetség (kereszteződés) tartói is nevezett egyesület (kereszteződés).
kivonás készletek
Legyen adott egy tetszőleges halmaz A és B
Definíció: A különbség a két A és B halmaza A \ B amelynek elemei tartoznak a halmaz, de nem tartozik a beállított B.
A \ B = X | x


Megmutatjuk a különbség a diagram az A és B Let:
1) A és B halmaz nem kerülnek kapcsolatban egymással.
Nyilvánvaló, hogy ebben az sluchaeA \ B = A és B \ A = B.
2) meghatározza az A és B viszonyában az egyenlőség.
3) az A és B van a felvétel.
Ha egy



4) az A és B viszonylatában kereszteződés.
Kikelés mutatja elemek sokaságát tartozó \ B.
Definíció szerint, a különbség a két készlet A \ B = A; b>. mert csak ezek az elemek tartoznak a halmaz és B halmaz - nincs.
Mivel N


Megjegyzés: Ha a B halmaz egy részhalmaza A. különbség A \ B a komplementere a B halmaz beállítani az A és B-vel jelöljük
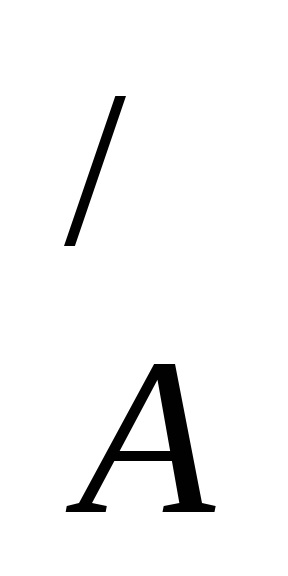
az


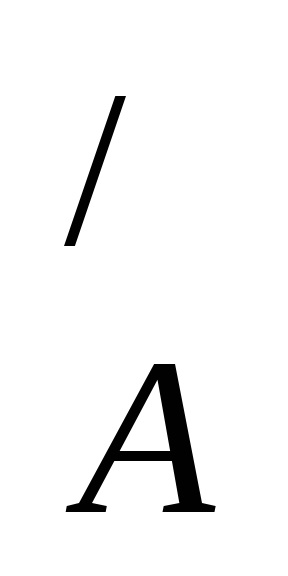
Ha A - az univerzális készlet (J), akkor a különbség J \ B = B

1) Legyen A = a; b>, B =. Ha lehetséges, a mellett a B-A vagy A-B
Mivel egy


Mivel N


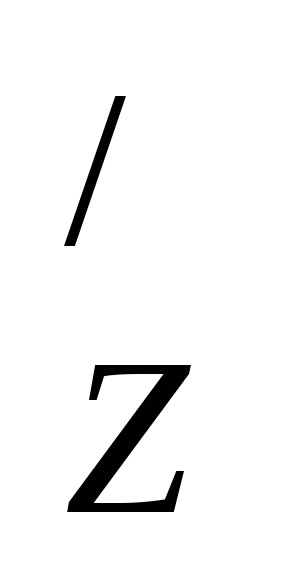

Megjegyzés: Ahhoz, hogy határozza meg a valós számok halmaza, speciális szimbólumokat használjuk: numerikus időközönként. Például,
[A; b] = x | x



[A; b) = x | x



(A; b] = x | x


(A; B) = x | x

Ezek az intervallumok - ez egy részhalmaza a valós számokat.