Megoldjuk tipikus problémák analitikus geometria

Tekintsük az elvet problémák megoldására a témában. „Egy egyenes a síkban, meg az egyenlet egy egyenes, amely áthalad egy adott ponton, a megállapítás metszéspontjait szögfelezői szögek, stb.”

Tekintsük az alábbi problémát példaként

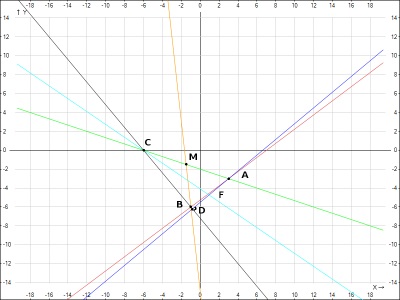
Példa: adott koordinátáit a csúcsai a háromszög \ (ABC \) \ (A (3; -3), B (1; -6), C (-6; 0) \)

1. Tedd az egyenlet a háromszög oldalai.
   
2. megtalálni az egyenlet
   
   
   
   1. magassága \ (AD \),
      
   2. medián \ (BM \),
      
   3. felezővonal \ (CF \).
      
   
   
3. Olyan rendszert hozzon létre az egyenlőtlenségek, oldatok, amelynek ez a készlet minden háromszög pontjait \ (ABC \).
   
4. Keresse szög \ (B \) radiánban legfeljebb két számjegy.
   
5. Készíts egy rajzot.
   

1. Tedd az egyenlet a háromszög oldalai. A fordításhoz az egyenlet a háromszög oldalai érintették a feltétele a problémát. Abban az állapotban, adott koordinátáit három csúcsa a háromszög, azaz a összeállításához egyenletek a vonalak \ (AB, BC, CD \) kapnak 2 pontot, amelyen keresztül a vonalakat át. Ahhoz, hogy használni egyenlet megoldások átmenő a két adott pont $$ \ frac = \ frac $$ ahol \ ((x_1; y_1) \) - koordinátáit az első ismert pont, \ ((x_2; y_2) \) - egy második ismert pont koordinátái . Mi helyettesítheti a koordinátákat, és így a egyenes egyenlete
   közvetlen \ (AB \). áthalad a ponton \ (A (3; -3), B (-1; -6) \), alkotják az egyenlet $$ \ frac = \ frac => \ frac = \ frac => y = \ fracx- \ frac $ kaptunk $ lineáris egyenlet \ (AB \). Az egyenlet közvetlen veszi lejtőn \ (k_ = \ frac \), amely szükséges a következő problémákat.
   közvetlen \ (BC \). Ez áthalad a ponton \ (B (1; -6), C (-6; 0) \) alkotják az egyenlet $$ \ frac = \ frac => \ frac = \ frac => y = - \ fracx- \ frac $$ kapott lineáris egyenlet \ (BC \). Az egyenletben, tudomásul vesszük a lejtőn az egyenes \ (k_ = - \ frac \), amely szükséges a következő feladatokat.
   közvetlen \ (AC \). áthalad a ponton \ (A (3; -3); C (-6; 0) \) alkotják az egyenlet $$ \ frac = \ frac => \ frac = \ frac => y = - \ fracx-2 $$ kaptunk a vonal egyenlete \ (AC \). Az egyenletben, tudomásul vesszük a lejtőn az egyenes \ (k_ = - \ frac \), amely szükséges a következő feladatokat.
   
2. megtalálni az egyenlet
   
   
   
   1. magassága \ (AD \). magasságú egyenlet ismerjük a koordinátáit csak egy pontot - \ (A (3; 3) \), így használjuk egyenlet egyenes, amely áthalad egy adott pont egy adott irányban. $$ y-y_0 = k_ (x-x_0) $$. ahol \ ((x_0; y_0) \) - a koordinátáit egy ismert pont, és \ (k_ \) - a lejtőn. Ebben az egyenletben nem tudjuk csak a lejtőn. Találni, erre használjuk a tulajdonát merőlegesek. Közvetlen \ (AD \ bot BC \). Jegyezzük fel a tulajdonságok \ (k_ * k_ = -1 => k _ * (- \ frac) = -1 => k _ = \ frac \). Construct az egyenlet a sor \ (AD \) $$ y - (- 3) = \ frac (X-3) => y = \ fracx- \ frac $$
      
   2. medián \ (BM \), a medián egyenlet a problémát találni egy adott koordináta pont \ (B (1; -6) \), és az is ismert, hogy a medián osztja az ellenkező irányba a fele. Megtaláljuk a pont koordinátáit \ (M \). Ehhez használja a képlet a pont koordinátáit, amely elválasztja az intervallum \ (AC \) egy előre meghatározott arányban \ (\ lambda \), ahol a \ (\ lambda = \ frac = \ frac = 1 \), és a koordinátákat \ ((x_1; y_1) , (x_2; y_2) \) - a koordinátákat a végpontok, amely elválasztja pont \ (M \) t.e.tochek \ (a (3; -3); C (-6; 0) \) helyettesítő és kap $ $ x = \ frac = \ frac = - \ frac $$$$ y = \ frac = \ frac = - \ frac $$ kapott pont koordinátáit \ (M (- \ frac; - \ frac) \). Kaptunk két pontot, amelyen keresztül az egyenes egyenletét használatra egyenlet áthaladó egyenes vonal két pont megadott \ (\ frac = \ frac \), helyettesítjük pontok koordinátáinak \ (B (1; -6), M (- \ frac; - \ frac) \), és megszerezni $$ \ frac + 6> = \ frac + 1> => y = -9x-15 $$
      
   3. szögfelező \ (CF \), hogy megtalálja az egyenlet a felezővonal használat tulajdonát felezővonal szög a háromszög: a belső felezővonal a szög a háromszög egyenlő részre osztja a szemközti oldalon a sarokban szegmensekre, amelyek arányosak a másik két oldal a \ (\ frac = \ frac \), azaz így találunk tényező \ (\ lambda \), majd a képlet a pont koordinátáit, amely elválasztja az intervallum \ (AB \) egy előre meghatározott arányban \ (\ lambda \), és megtalálni a pont koordinátáit \ (F \) és az utolsó helyettesítő származtatott koordináták az egyenes egyenlete áthaladó két megadott pont.
   Kezdjük: megtalálni a szegmensek hossza \ (AC \) \ (BC \). $$ AC = \ sqrt = \ sqrt = \ sqrt = \ sqrt $$$$ BC = \ sqrt = \ sqrt = \ sqrt = \ sqrt $$ most találjuk együttható \ (\ lambda = \ frac = \ frac = \ sqrt > \). Azt találjuk, a pont koordinátáit \ (F \) át ismert koordinátáit a végpontok \ (AB \) \ (A (3; -3), B (-1; -6) \) $$ x = \ frac = \ frac >>> > $$$$ y = \ frac = \ frac >>>> $$ kapott két pontot, amelyen keresztül vonal \ (CF \), az egyenlet közvetlen \ (CF \) használja egyenlet áthaladó egyenes vonal a két pontot definiált \ (\ frac = \ frac \), helyettesítjük pontok koordinátáinak \ (C (-6; 0), F (\ frac >>>>; \ frac >>>>) \), és megszerezni $$ \ frac >>> > -0> = \ frac >>>> + 6> => \ frac >>>>> = \ frac> + 6 + 6 * \ sqrt >>>>> => $$$$ \ frac >> = \ frac >> => $$$$ y = \ frac >> * (- 3-6 * \ sqrt>) => $$$$ y = - \ frac >>>> * X-18 \ frac >> >> $$
   

Készíts egy rajzot.