Meghatározása rugalmassága gumi modulok - fizikai workshop - fizika órák 10. évfolyamon
A gyakorlati munka № 5
Témát. Meghatározása a rugalmassági modulus, gumi
Célkitűzés: A kísérleti ellenőrzésére Hooke-törvény határozza meg a rugalmassági modulus gumi.
Készülékek és anyagok: gumi szalag hossza 20-30 cm; Állítsa be a súlyok 102 g; mérő vonalzó egy skálán 5 mm / a; Univerzális állvány aljzat és a láb; féknyereg.
Ha van deformáció a test rugalmas erő. A kis deformációk rugalmas erőt hoz létre mechanikai igénybevétel σ, egyenesen arányos a törzzsel ε. Ezt az összefüggést nevezzük Hooke-törvény, és a következő formában:
ahol σ = F / S; F - az erő a rugalmasság; S - a keresztmetszeti területe a minta; l - l 0 - abszolút deformáció; l 0 - kiindulási minta hossza; l - hossza kifeszített próbadarab; E = σ / ε-rugalmassági modulus (Young). Ez jellemzi a képessége egy anyag ellenáll a deformációnak és számszerűen egyenlő a mechanikai stressz ε = 1 (azaz, ha L = 2 l 0). Igazán nem állhatom ezt a törzset nincs szilárd és meg kell semmisíteni. Már jelentős alakváltozás megszűnik és hajlékony, Hooke-törvény nem érvényes. Minél nagyobb a Young-modulus, a kevésbé deformált rúd azonos feltételek mellett (azonos F. S. l 0).
1. nóniuszos tolómércével mérjük meg a D átmérője a gumi szalagok és kiszámítja annak keresztmetszeti területe általános képletű:
2. Csatlakoztassa a szabad végét a gumi szalag az állványban, és mérjük azt a vonalzóval eredeti hosszát L 0 az alsó széle az állvány lábait, hogy helyezze tyagartsya rögzítő.
3. szuszpendáló, hogy az alján a súlyok kapcsolja hurok (ábra. 1), a mérést minden alkalommal egy új L hossza gumicsík. Számítsuk ki az abszolút nyúlási csíkok: l - l 0.
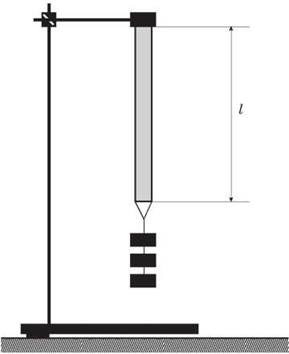
4. Határozza meg az alkalmazott erő F = mg. ahol g = 9,8 m / c 2. Eredmények rekordot a táblázatban.
5. A kapott adatok össze egy grafikon, a stressz σ a nyúlás ε.
6. Jelölje ki a grafikon szögletes rész és belül, kiszámítja a modulusa képlet:
7. Számítsa abszolút és relatív mérési hiba Young-modulusa az egyik pontot, hogy tartoznak az egyenes szakasz a diagram, képletekkel:
ahol Δ F = 0,05 H, Δ L = 1,5 mm, Δ D = 0,1 mm; AE = Eε.
8. Vedd az eredmény a következő formában:
9. Készítsen következtetést a munka.
1. Miért van az modulusa van kifejezve annyi?
2. Miért nem határozható meg modulus közvetlen mérés definíció?