Március 2. összegét számítja ki egy végtelen sorozat

3. A gyűrűs szerkezeteket a program

Összegét számítja ki egy végtelen sorozat egy adott pontosság

Adott egy számsorozatot R1. R2. R3, ..., Rn, .... Expressziója R1 + R2 + R3 + ... + Rn + ... nazyvayutbeskonechnym következő. vagy prostoryadom. és a szám R1. R2. R3, ... tagállamait a sorozat. Ebben az esetben szem előtt tartani, hogy az összeg a sorozat kezdődik a felhalmozási első tagjai. Összeg Sn =

nazyvaetsyachastichnoy summoyryada. ha n = 1 - egy első részleges összeget, ha n = 2 - a második részleges összeget, és így tovább.

Ez a sorozat konvergens. ha a szekvenciát részleges összegek van egy határ iraskhodyaschimsya - egyébként. A koncepció az összeg a szám lehet hosszabbítani [9], majd néhány eltérő sorozat is lesz összegeket. Imennorasshirennoeponimaniesummyryada fogják használni a fejlesztés algoritmusok a következő probléma: a felhalmozási összegeket kell végezni mindaddig, amíg egy rendes tagja számos abszolút értéke nagyobb, mint egy előre meghatározott érték ε.

Általában részben vagy egészben a feltételeket a sorozat lehet adott kifejezéseket, amelyek függnek a száma a tagok száma és a változók. Például,

Felmerül a kérdés, hogy minimálisra csökkentsék az összeg a számítás - az A értékét a következő kifejezés a sorozat általános képletű a tagok száma (a fenti példában ez egy kifejezést összege) a rekurzív képletű (ez kimenete alább látható), vagy használja megismétlődik képlet csak expresszáltatására számos tagja egységek (cm. alább).

Következtetés kiújulás képlete: a tagok száma

Tegyük fel, hogy meg akarja találni egy számsorozat R1. R2. R3, ..., egymás után ezek kiszámítására képletek szerint

,, ...,

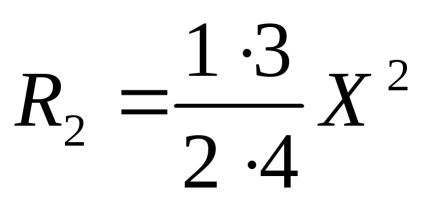
Hogy csökkentse a számítás ebben az esetben célszerű használni rekurrentnoyformuloy fajtája, amely lehetővé teszi, hogy az A értékét RN N> 1, ismerve az érték az előző tag számos RN-1. ahol

- kifejezés, amely lehet után kapott egyszerűsítése expresszió vonatkozásában az (3.1) az N expressziós az N-1:

Így a rekurziós képlet válik.

Összehasonlítása alapján az összes tagok száma általános képletű (3,1) és visszatérő (3.2), amely nagymértékben egyszerűsíti a kiújulás képlet számítás. Alkalmazható N = 2, 3 és 4 tudjuk, hogy

:

Az eljárás értékének kiszámításakor számos tagja

Kiszámításához értékeit tekintve a sorozat, a típusától függően, előnyös lehet, hogy egy tagja számos általános képletű vagy kiújulás képletű, vagy egy vegyes számítási módszerét az értékek számos tagja. amikor egy vagy több a számos elem részek kiújulásának képleteket használunk, akkor azok értéket behelyettesítjük általános képletű sorozat tagja. Például - ryadaprosche értékének kiszámításához számos tagja

ő általános képlet(Vö- rekurziós képlet); - ryadaluchshe használni a kiújulás képletű; - alkalmazni kevert módszert ryadasleduet kiszámítjuk = X 3 n a kiújulás képletű , N = 2, 3, ..., ha A1 = 1, és BN = N! - továbbá a kiújulás képletű , N = 2, 3, ... amikor a B1 = 1, majd - tagja számos- szerint az általános képletű, amely azt feltételezi, formájában.

Példa 3.2.1 Quest

Számolja precíziós ε 0 o X45 o

A közelítő értékeit cos X a következő képlet szerint:

egy rekurzív számítási képlete a tagok száma:

,

A pontos érték a függvény cos X,

az abszolút és relatív hibája közelítő értékek.