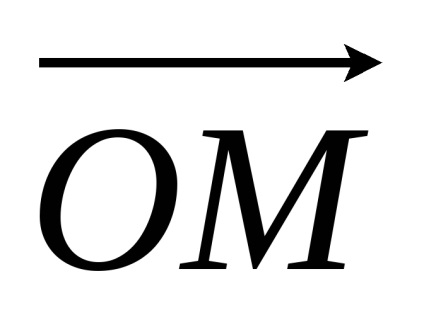
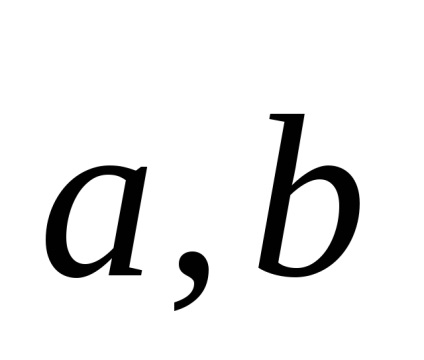Lineáris műveleteket vektorok
Alapfogalmak vektor algebra
Skalár és vektor mennyiségek
Természetesen elemi fizika ismert, hogy bizonyos fizikai mennyiségek, mint a hőmérséklet, térfogat, tömeg, sűrűség, stb esetben csak egy számértéket. Ezeket a mennyiségeket nevezzük skalárnak vagy skalár.
Annak megállapításához, a más mennyiségek, mint például erő, sebesség, gyorsulás és hasonlók, továbbá a numerikus értékeket, meg kell kérni a másik, és irány az űrben. Értékek, melyek amellett, hogy az abszolút érték is jellemzi az irányt nevezett vektort.
OpredelenieVektorom úgynevezett irányított szegmenst, amely által meghatározott két pont: az első pont meghatározza az elején a vektor, és a második - a végén. Ezért azt mondják, hogy egy vektor - egy rendezett pár pontot.
Az ábra van ábrázolt egy vonalszakasz vektor, amelyben a nyíl irányában jelölt elején a vektor a végén. Például, ábra. 2.1.
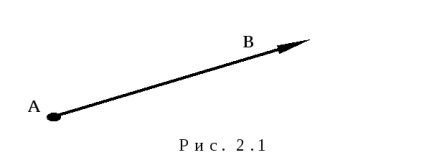

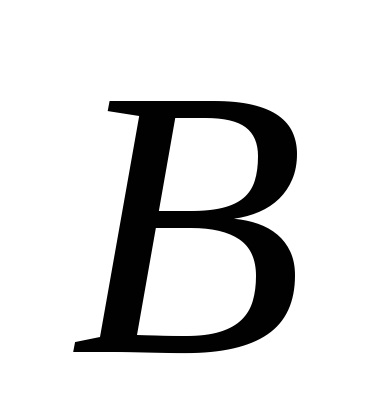
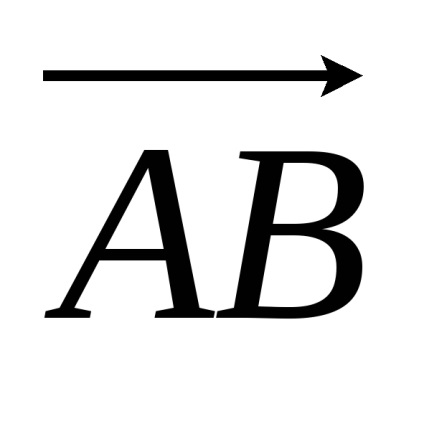

A vektorok közé tartoznak a nulla vektor. amelynek a kezdete és vége ugyanaz. Ez jelöli
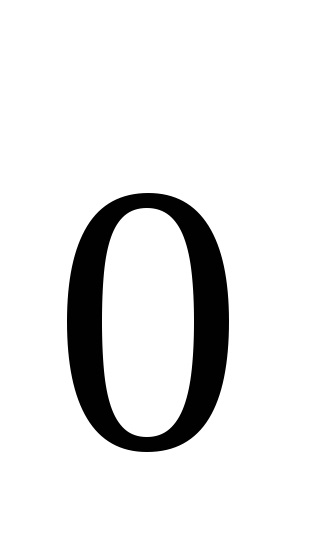
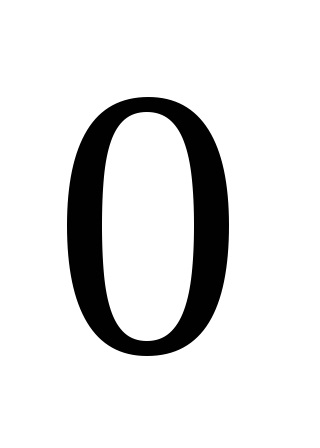
A távolság a kezdete és vége a vektor neve annak hossza, vagy a modul. vektor modul által jelzett két függőleges rudat balra:
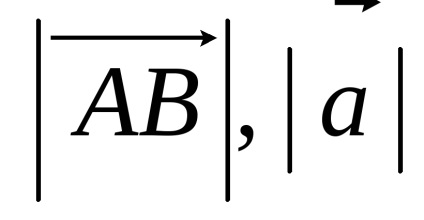

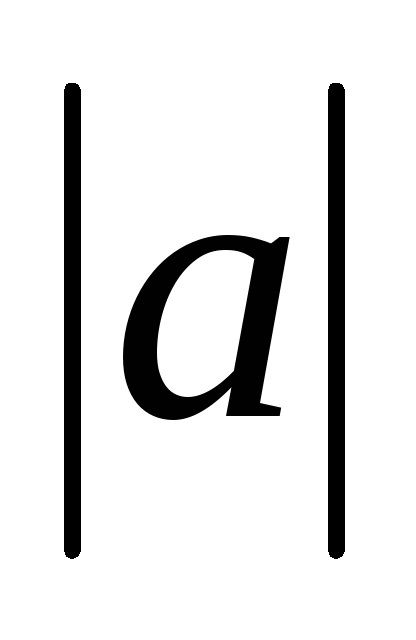
Vector párhuzamosan ugyanazon a vonalon hívják esik.
Vektor fekszenek ugyanabban a síkban vagy párhuzamos síkban helyezkednek nevezzük egy síkban vannak.
Nulla vektor minősül kollineáris bármely vektor. Hossza megegyezik a 0.
Definíció két vektor
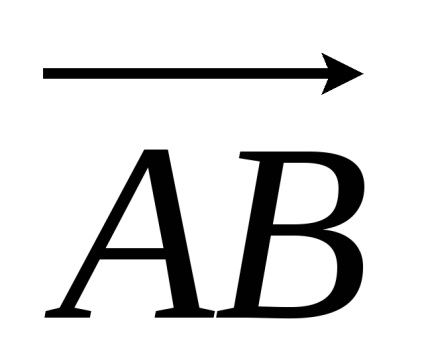
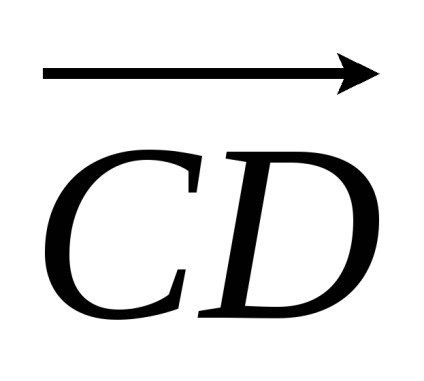
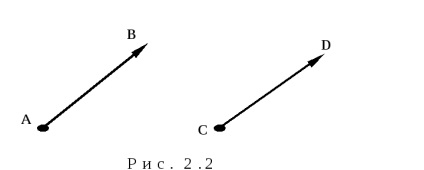
Ez van írva, mint:
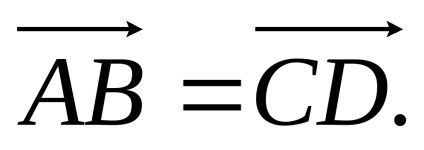
A meghatározása az egyenlő vektorok az következik, hogy a párhuzamos átvitel vektor olyan vektor, amely egyenlő a kezdeti, mert az elején a vektor lehet helyezni bármely pontján helyet. Az ilyen vektorok (elméleti mechanika geometria), amelynek kezdetén lehet elhelyezni a tér bármely pontján, az úgynevezett szabad. És ezek a vektorok fogjuk vizsgálni.
OpredelenieSistema vektorok
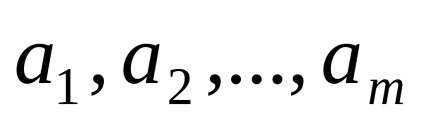
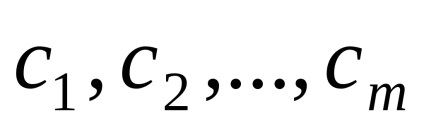
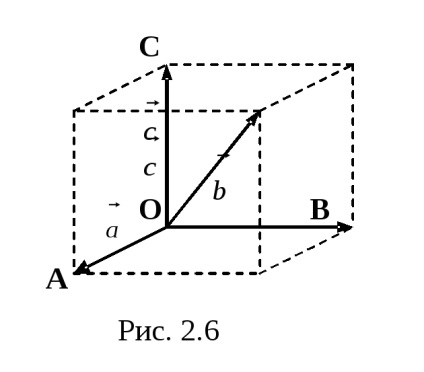
OpredelenieBazisom a térben említett tetszőleges három nem egy síkba eső vektorok, amelyek az elkészítve egymás.
OpredelenieEsli
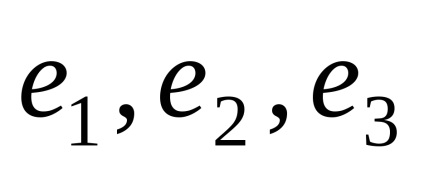
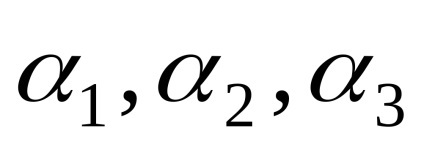

vektor koordinátái levelet zárójelek jel utáni vektor. Például,
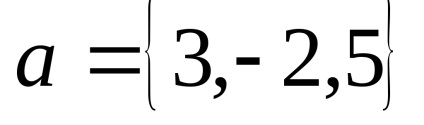

A tulajdonságait vektor szorzás számmal és hozzáadunk vektorok az állítás tekintetében lineáris műveletek alatt vektorok definiált koordinátákat.
Ahhoz, hogy megtalálja a koordinátákat a vektor, ha valaki ismeri a koordinátáit kezdete és vége kell, hogy legyen a megfelelő koordinátáit végén hozza koordináta elején.
Lineáris műveleteket vektorok úgynevezett felül (kivonás) a vektorok és a vektor szorzás számmal. Nézzük őket.
OpredelenieProizvedeniem vektor

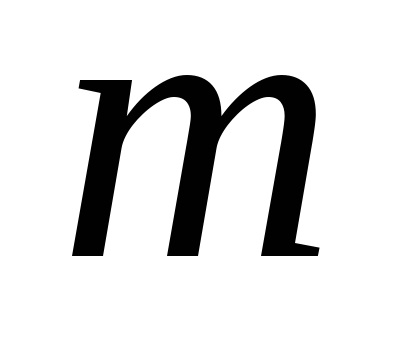

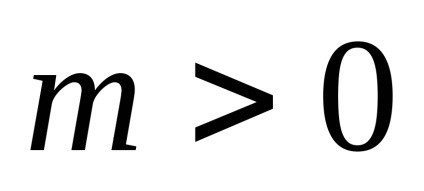
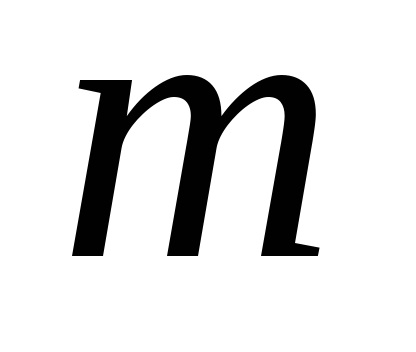

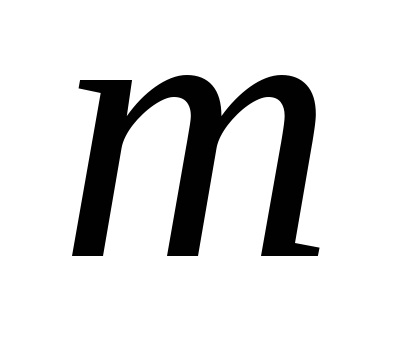
P
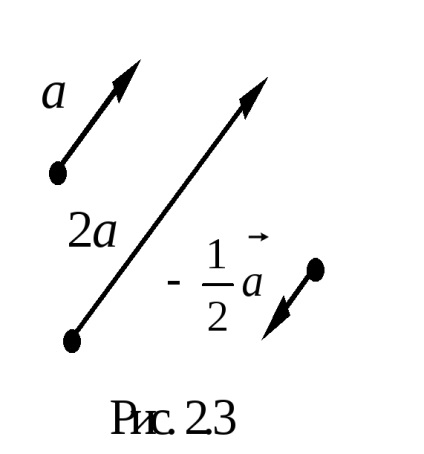
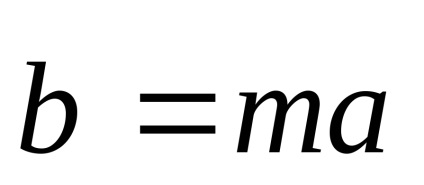
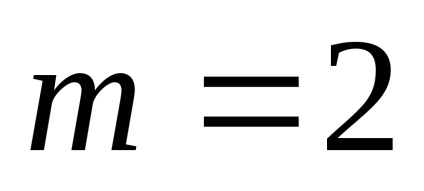
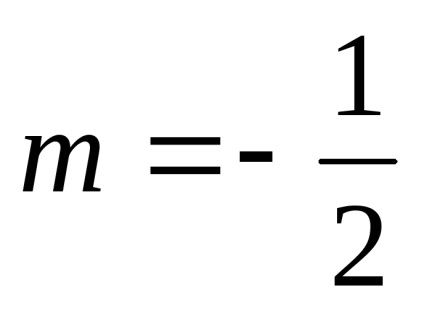
Ha megszorozzuk a vektor számos koordinátáit szorozni ezt a számot.
Valóban, ha a
.
terméket a vektor

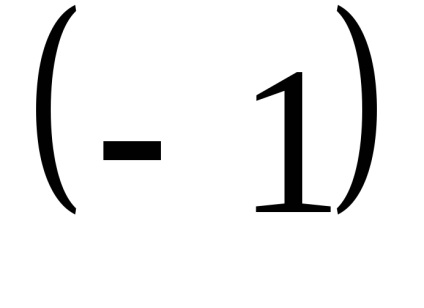
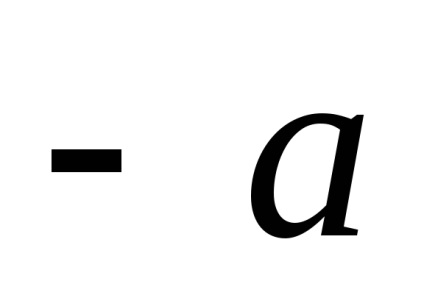
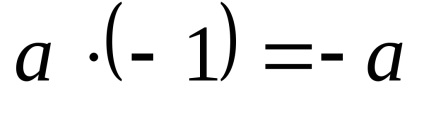

Megjegyezzük, hogy a vektor hossza egyenlő 1, úgynevezett egység (vagy az egység vektor).
Használata vektor szorzás művelet számos, bármilyen vektor lehet kifejezni egy egységvektor ugyanabban az irányban. Sőt, elosztjuk a vektor

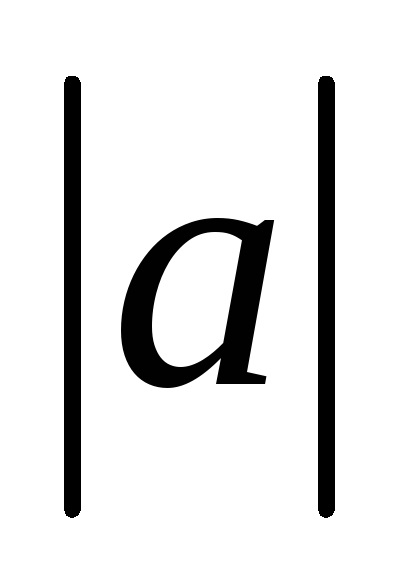

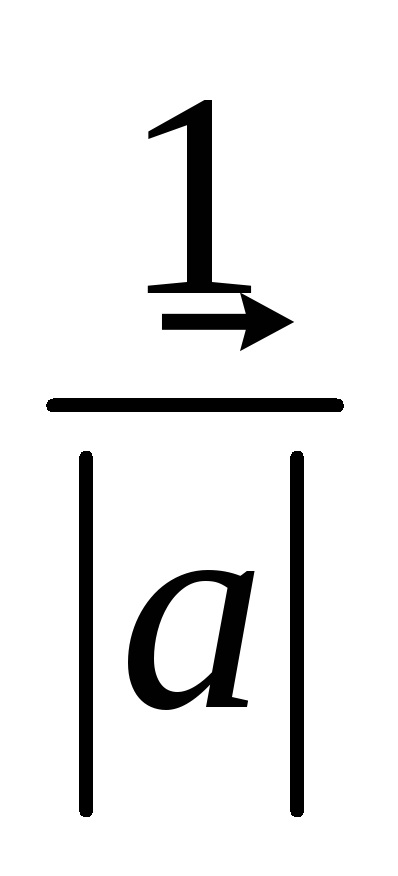

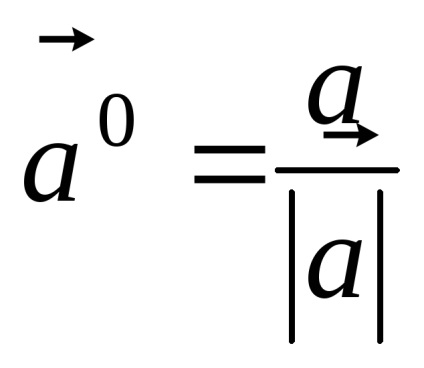
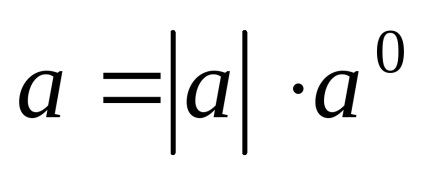
OpredelenieSummoy két vektor

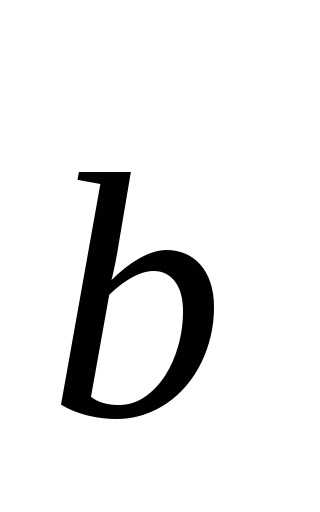


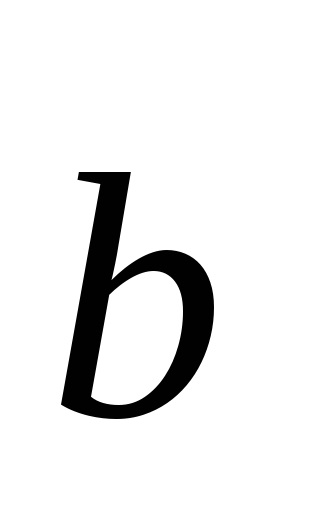
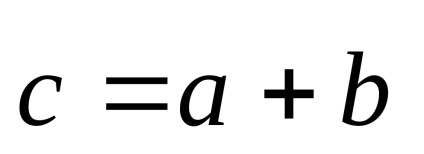
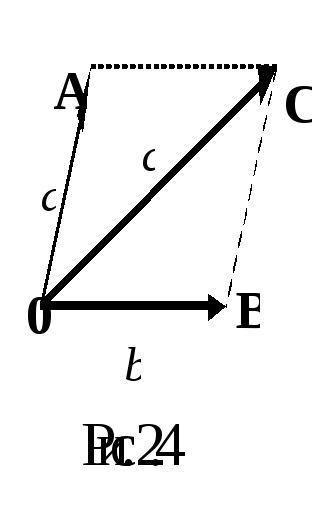
A meghatározás szerint, az egyenlő vektorok
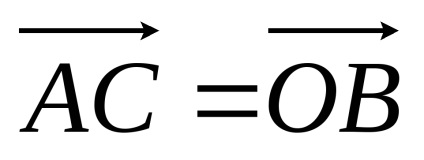


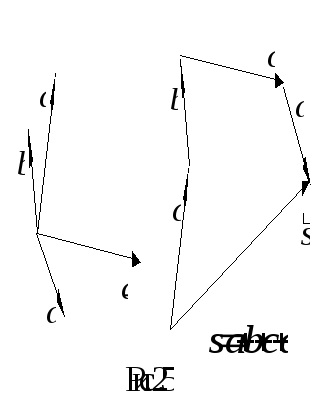
Így annak érdekében, hogy szükséges vektorok összege, szükséges csatolni a végén az első vektor elején a második, a végén a második csatolni az elején a harmadik, és így tovább. Ezután a vektor összeg, és lesz egy vektor, amely összeköti az elején az első a vektorok a végén az utóbbi.
Hozzáadásakor vektorokat adunk hozzá, és a hozzájuk tartozó koordinátái
Valóban, ha,
Ha a vektorok