Lecke „poliéder szög”
Szöveg kódolása tanulság:
A síkrajzi egyik tárgy tanulmányi szög.
Szög - mértani alakzat áll pontokat - a csúcspont és két sugár származó ezen a ponton.
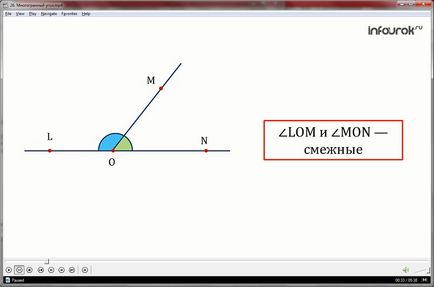
Két szög, egy párt, amely általános és a másik kettő a folytatása egy másik, az úgynevezett síkgeometria szomszédos.
Az iránytű lehet tekinteni, mint egy modell Síkszög.
Emlékezzünk a koncepció dihedráiis szög.
Ez a szám által alkotott vonal, és két fél sík a közös határt, és amelyek nem tartoznak ugyanabba a síkgeometria úgynevezett torziós szög. Half-sík - a szélén a torziós szög. Line - a borda a torziós szög.
A tető a ház bemutatja a torziós szög.
De a tető a ház az ábrán két formájában van egy alak által alkotott hat sík közös csúcsa szögek úgy, hogy a szögek hozzák egy bizonyos sorrendben, és az egyes szomszédos sarkok, beleértve az első és az utolsó, van egy közös oldalon. Hogy hívják ezt a formáját a tető?
A geometria alakja, amelynek tagjai a szögek
A1OA2, és így tovább A2OA3 AnOA1 és a belső régiók oly módon, hogy a szomszédos zónák nem egy síkban, hanem a szomszédos szögek (saját belső területek) nincs közös pont az úgynevezett poliéder szög OA1A2 A3 ... A n.
A sarkok, amelyekből ez a szöget nevezzük lapos sarokkal. Síkján szögek nevezzük széleit poliéder szög. Az O pont az úgynevezett a szög csúcspontját.
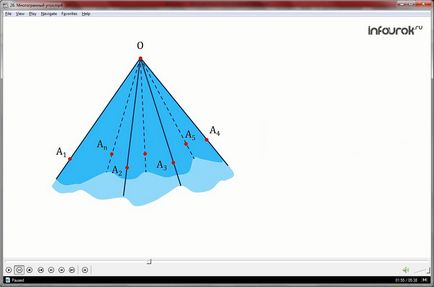
Példák a poliéderes szögek megtalálható a tetraéder és paralelepipedon.
Metszettel Tetrahedron DBA, ABC, DBC formában poliéderes szöget VADC. Leggyakrabban ez az úgynevezett háromoldalú szöget.
A AA1D1D paralelepipedon arcok, ABCD, AA1B1B generátorok háromszögletű szög AA1DB.
Nos, a tető, a ház készült formájában egy hatszög szög. Ez áll a hat sík szögek.
Polihidrális szög tart több tulajdonsággal rendelkezik. Mi kialakítsa és bizonyítani azokat. Itt azt írják, hogy a nyilatkozat

Először is, minden konvex poliéder szög van egy sík, amely metszi az összes bordája.
Tekintsük a bizonyítékok poliéderes szög OA1A2 A3 ... A n.
A hipotézis, hogy konvex. A szöget nevezzük konvex, ha annak egyik oldalán az síkja minden egyes sík szögek.
Mivel a hipotézis a domború sarokban, pontok O, A1, A2, A3, hogy An egyik oldalán a sík OA1A2
Döntetlen középvonali KM háromszög OA1A2 és válasszon OA3 élek OA4, oan a borda képező síkjával RCM, a legkisebb torziós szög. Legyen egy él OAI. (Oa itoe)
Tekintsük a fél-α CM határa elosztjuk a diéderes szöget OKMAi két diéderes szög. Minden csúcsot A-A n hazugság egyik oldalán sík α, és D pont a másik oldalon. Ezért α sík metszi minden éle a poliéder szög. Az az állítás bizonyított.
Konvex poliéder szögek van egy másik fontos tulajdonság.
Összeg planáris szögek a konvex poliéder szöge kisebb, mint 360 °.

Tekintsük egy konvex poliéder szöget vertex ponton O. A fenti állítások van egy sík, amely metszi minden széle.
Rajzolj egy síkban α, hagyjuk, hogy metszi a széleit a szög pont A1, A2, A3 An, és így tovább.
Sík α a külső területen vágandó síkszög háromszög. A szögek összege 180 °. Azt látjuk, hogy az összeg a sík szöge A1OA2 hogy AnOA1 kifejezést átalakul ebbe a kifejezésbe átrendezni szempontjából, megkapjuk
Ebben a kifejezésben összegek a zárójelben szereplő összegek lapos háromszögletű sarok szögek, s mint tudjuk, ők nagyobb, mint a harmadik sík szögét.
Ez az egyenlőtlenség lehet írni az összes háromoldalú sarkok kialakítására poliéder szöget.
Következésképpen, megkapjuk a folytatása az egyenlőség
A kapott válasz azt mutatja, hogy az összeg a sík szögek a konvex poliéder szög kisebb, mint 360 fok.