Láncok és ciklusok grafikonok
Mozgó szélei mentén G (X, U), akkor mozog a csúcs a csúcs. Bármilyen szekvenciája élek kapott egyidejűleg nevezzük útvonalat. azaz szekvenciát (x0, x1) (x1, x2) ... (xn, xn -1), ahol bármely két szomszédos borda szomszédos - útvonalon.
Lánc - olyan útvonal, amely a szélek különböző.
Egyszerű lánc - lánc, amelyben az összes csúcsot különbözőek.
Ciklus - lánc, amelyben ugyanaz a kezdő és befejező csúcsok.
Tree - összefüggő gráf nélkül ciklusokat. A fa, bármely két pont között egy láncot. Fa épített n pontú n-1 éle.
Fa - egy sor fák.
A grafikonok két gyönyörű ciklus: Euler és Hamilton.
Gróf nazyvaetsyaeylerovym. ha minden csúcsa a grafikon van az útvonal kezdődik és ér véget a vertex és átmegy minden él csak egyszer. Egy ilyen út az úgynevezett Euler ciklust.
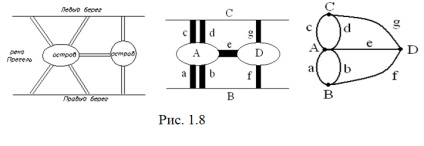
A probléma abból adódott, a következő példát. A XIII században lakói Königsberg, séta át a hidak folyó Pregel próbálta megoldani a problémát: Lehetséges, hogy kb minden hidat, továbbadása mindegyik csak egyszer (1.8 ábra).
A feladat a következő. végezzen egy sétát a városban, így elhagyása után pontosan egyszer minden hidat, hogy visszatérjen az ugyanazon a helyen, ahol a séta kezdődött. E probléma megoldása, Euler Königsberg ábrázolt, mint egy grafikon, azonosítja azt a felső részét a város, és az élek - a hidak, amelyek ezekhez a részek.
Euler sikerült bizonyítani, hogy a kívánt útvonal elkerüli a város nem létezik.
A válasz lehet beszerezni alapján az alábbi tétel.
Tétel. Egy gráf Euler akkor és csak akkor, ha a fokozatok minden csúcsa még.
Mint látható az ábrán, a gróf áramkör szimulátor hidak, minden csúcsának a páratlan fokú. Következésképpen Euler ciklus ebben a grafikonban nem létezik.
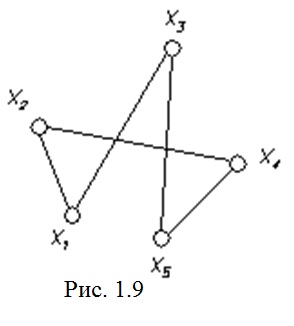
Példa grafikon, amelynek Euler ciklus ábrán látható. 1.9.
Egy gráf Hamilton. if (összes élei nem vesz részt ebben az esetben) van az útvonal kezdődik és fejeződik be a felső és áthalad a csúcsot csak egyszer minden csúcsa a grafikon. Ez az útvonal az úgynevezett Hamilton kör.
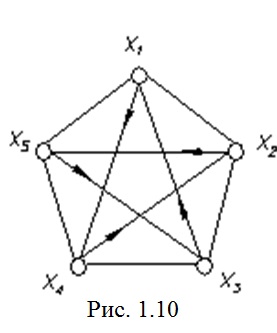
A teljes gráf csúcsainak számát n »2 mindig létezik Hamilton kör. Egy példa egy ilyen ciklus ábrán látható. 1,10 - (x1, x4) (X4, X2) (X2, x5) (x5, x3) (x3, x1).
Hamilton-grafikonok modellezéséhez használt számos gyakorlati probléma, például, modellként szolgálhat a készítményben a menetrendek. Az alapja az összes ezeket a problémákat egy klasszikus utazó ügynök probléma: az eladó köteles bejárjuk a várost, és a hátsó, látogatás minden városban pontosan egyszer, ugyanakkor csökkenti a szállítás költségét a minimumra.
Grafikus modellje az utazó ügynök probléma Hamilton gráf, amelynek csúcsai képviseli a várost, és a szélek - összekötő őket az útra. Továbbá minden borda van szerelve egy súlyt jelzi szállítási költségek kell utazni a megfelelő módon, mint például a távolságot a városok, illetve a mozgás az úton. A probléma megoldása érdekében meg kell találni azt a Hamilton-kör minimális összsúlyú.