Középső sorban a háromszög

Tekintsük az ABC háromszög $ $, ahol $ _1 \ ~ 1 \ _1 $ mediánja. Mivel a medián oszlik két oldala van. Tekintsük a középvonal $ A_1B_1 $ (3.).

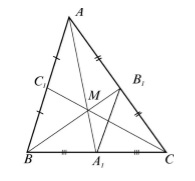
3. ábra illusztráció Következmény 1

By tétel 1, $ AB || A_1B_1 $ és $ AB = 2A_1B_1 $ ezért $ \ szög ABB_1 = \ angle BB_1A_1, \ \ angle BAA_1 = \ angle AA_1B_1 $. Tehát háromszögek ABM $ $ és $ A_1B_1M $ hasonló az első hasonlóság alapján háromszögek. majd

Hasonlóképpen azt bizonyítják, hogy

Következmény 2: A három középső sorban a háromszög osszuk 4 háromszöget, az eredetihez hasonló háromszög hasonlósági koefficiens $ k = \ frac $.

Tekintsük a háromszög $ ABC $ középpontú vonalak $ A_1B_1 \ _1C_1 \ B_1C_1 $ (4.)

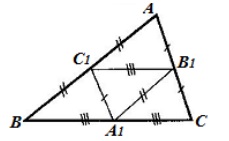
4. ábra illusztráció Corollárium 2

Vegyünk például egy háromszög $ A_1B_1C $. Mivel $ A_1B_1 $ - átlagos sor, a

Angle $ C $ - teljes szög a háromszög. Ennek megfelelően, háromszög $ A_1B_1C $ és $ ABC $ hasonló a második funkció hasonló háromszögek hasonlósági koefficiens $ k = \ frac $.

Hasonlóképpen tudjuk bizonyítani, hogy a háromszögek $ A_1C_1B $ és $ ABC $, és a háromszög $ C_1B_1A $ és $ ABC $ hasonlóak az hasonlósági koefficiens $ k = \ frac $.

Vegyünk például egy háromszög $ A_1B_1C_1 $. Mivel $ A_1B_1 \ _1C_1 \ B_1C_1 $ - átlagos sorában a háromszög, a

Következésképpen, szerint egy harmadik aspektusa a hasonlósága háromszögek, a háromszögek $ A_1B_1C_1 $ és $ ABC $ hasonló a hasonlósági koefficiens $ k = \ frac $.

Példák célok a koncepció a középső sor a háromszög

Dan oldalú háromszög $ 16 $ cm, $ 10 cm $ és $ 14 $ cm. Keresse meg a háromszög kerületét, amelynek csúcsai a közepén a háromszög oldalainak.

Mivel az a háromszög csúcsait kívánatos a közepén az oldalán a háromszög, a kéz - középvonala az eredeti háromszög. By Következmény 2, azt találjuk, hogy a kívánt oldalon a háromszög egyenlő $ 8 $ cm $ 5 $ cm $ 7 $ cm.

Dan háromszög $ ABC $. Point of $ n \ és \ M $ - $ felezőpontja az BC $ és $ AB $, illetve (5. ábra).

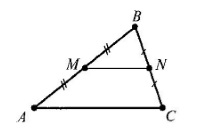
Kerülete a háromszög $ BMN = 14 $ cm. Keresse meg a kerülete a háromszög az ABC $ $.

Mivel a $ N \ és \ M $ - $ felezőpontja BC $ és $ AB $, akkor $ MN $ - átlagos vonalon. így

By tétel 1, $ AC = 2mn $. kapjuk: