Következtetés dolgozik képlet a kiszámítsuk a fajlagos töltés elektron
1. kenotrons 2TS2S típus egy állványon
3. A 2. ampermér
4. milliammeter 10 mA
5. A voltmérő 300 V
Cél: annak meghatározása, konkrét díjat az elektron által magnetron
Rövid elméleti információk
Közvetlen mérési tömegének az elektron jelentős probléma, mert a kicsiség. Ez sokkal könnyebb, hogy meghatározza a külön díj az elektron, azaz az arány a töltés mennyisége az e / m súlyt. és a nagysága a töltés a külön díj e, és m tömegű megtalálható elektron. Annak megállapításához, a e / m alkalmazhatunk különböző módszerekkel. Ebben a dolgozatban alkalmazott módszer magnetron.
A magnetron egy két elektróda vákuum cső katód egy hengeres és koaxiális vele a hengeres anód. A lámpát helyezünk egy homogén mágneses mező erővonalai vektor párhuzamos alkotó elektródák irányított, a indukciós.
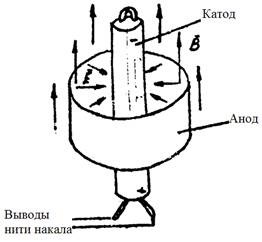
A katód izzószál felmelegszik, és a kibocsátott (durranógázt) az elektronok. Ha az elektródák csatlakoztassa az áramforrás ( „+”, hogy az anód „-”, hogy a katód), a rés között kialakított elektródák az elektromos erővonalak, amelyek a feszültség kerül sugárirányban az anód és a katód. Így az elektromos mező által, az elektronok jár erő:
ahol e - a töltés egy elektron;
E - elektromos mező vektort. A „-” jel azt jelzi, hogy a töltés az elektron - negatív.
Változás a kinetikus energia az elektron ahogy mozog az erő Fk lehet a következő képlettel:
ahol # 966; 1. # 966; 2 - potenciális különbség az eredeti és végső pont az út;
v1. v2 - a kezdeti és a végső elektron sebessége
Az elektron mozog mágneses mezőben, a Lorentz-erő hat, meghajlik röppályája. A nagyságát és irányát a Lorentz-féle erő formula határozza meg:
ahol Fl - vektor a Lorentz-erő;
v - sebességvektor;
B - mágneses indukció vektor.
A 2. ábra egy keresztmetszeti nézete a magnetron, ahol a és b - a sugara a katód és az anód. Az elektródák egy potenciális különbség. A mágneses mező merőleges a rajz az olvasó számára. Mozgó elektron a C pontban működtetőerő Fk és Fl. Az erő Fk mentén irányul sugara az anód. Az erőssége a Fl. képlet szerint (2), amely merőleges a vektor az elektron sebesség és a mágneses mező indukcióvektor B. erők iránya Fk és Fl a 2. ábrán látható. Mivel mindkét erők síkjában a rajz, az elektron mozgás határozza meg egy lapos spirális változó görbületi sugár, hogy sebességétől függ az elektron.
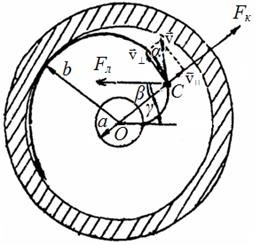
Az egyszerűség kedvéért feltételezzük, hogy a kezdeti sebesség az elektron a katódon v = 0.
Amikor a B = 0 az elektron erő Fk. elektron mozgás (tekintve la = 0) lesz egyenes vonalú a sugár mentén (3A.). Ebben az esetben minden elektronok által kibocsátott a katód, eléri az anód, ami az anód aktuális Ia.
Ha B> 0 egy elektron, de erő Fk. Ez lesz egy erő Fl Lorenz. hajlik a pályáját a mozgás az elektron. Ha B a kis, a görbület a pálya kicsi, és minden az elektronok eléri az anód (ábra. 3b).
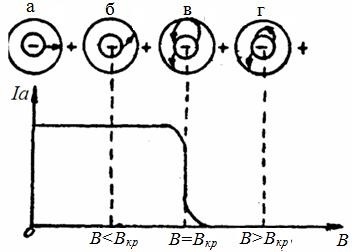
Ábra. 3. függése az anód áram a magnetron
a nagysága a mágneses indukció
A növekedés a pálya meghajolhat több és egy bizonyos „kritikus” értéke B = Bcr elektron pályája lenne érintő a felületére az anód (ábra. Sv). Amikor a B> Bcr. röppálya görbületi lesz olyan nagy, hogy levették a katód, az elektron leírja egy görbét, ismét véget a katód (3A.). A sebesség idején visszatérés a katód nullára csökken, ami után az elektron mozog az anód. Mivel ebben az esetben nincs elektron eléri az anód, az anód la áram nulla.
Tehát, ha a<Вкр величина анодного тока не зависит от В. а при В>WRC anódáram egyáltalán megáll. Amikor B = Bcr. van egy éles csökkenés (reset) az anód áram nullára (ábra. Sv). Ismerve az SRS. Megtalálható az arány e / m.
Következtetés dolgozik képlet a kiszámítsuk a fajlagos töltés elektron
Feltételezzük, hogy a B = Bcr és így az elektron pályáját érintő a felületére az anód (2. ábra). Bemutatjuk polárkoordináták: rádiuszvektorhoz r (r = OC), és a sugara vektor elfordulási szög # 966; képest a függőleges irányban OA.
Electron sebesség v vektor bontható komponense merőleges a sugara, és egy alkatrész irányított sugár mentén. Úgy véljük, hogy az eltérés a katód, amikor r = 0, VRA = v # 966; a = 0.
Ha R = b elektron pályája érintője az anód. Következésképpen, VRB = 0, v # 966; b = Vb. Egy érintési pont r = b írhatók a következő képlet szerint:
ahol az UA - közötti potenciálkülönbség az anód és a katód.
Annak meghatározására, f / m az egyenlet nem elég, mert ismeretlen értéket. Szerint a második törvénye dinamika forgómozgást van:
Abban a pillanatban az elektron bármikor is:
Az erőssége a Fe pillanat nem hozza létre, mint sorában a fellépés átmegy a ponton O. Ezért a pillanatban a ható erő az elektron, adják csak ereje által Fl (2. ábra).
Mivel ebben az esetben: Fl = evVkr (lásd (2) képletű, akkor .:
Ábra. 3. ezt. ezért:
A termék felírható:
Ezután, a (5) egyenlet a (6) és (9) kapjuk:
Ez a kifejezés jelenti az egyenlőség a származékos a két funkció. mert függvény, amelynek származékok, esetleg csak egy additív konstans, írhatunk:
A C konstans lehet meghatározni a kezdeti feltételek. Ha R = 0. v # 966; = 0.
Ezután eVkr egy 2 + C = 0. ahol:
Behelyettesítve az értéke C (11), azt látjuk, a kapcsolat v # 966; a sugár minden egyes pontja a pálya:
Emelése v # 966; b négyzetének és helyettesítésével a (4), kapjuk:
Ebből másodfokú egyenlet megtalálható e / m. Mivel a megoldás e / m = 0 nem érdekel minket, azt találjuk:
Szerelési (ábra. 4) egy szelep cső típusú 2TS2S 1, a műszerfalon szorítóbilincsek 3, van kötve a lámpa panel. A lámpa kerül a mágnesszelep 4, amely egy többrétegű tekercs 5 seb egy nemmágneses 6 keret, a terminálok 7 használják az elektromágnes bekapcsolását.
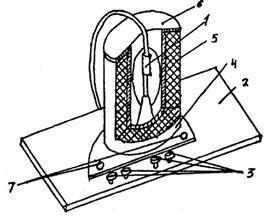
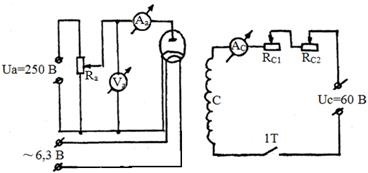
Ábra. 4. Telepítés típusa ábra. 5. sematikus ábrája a telepítés
Elektromos szerelési rajz ábrán adtuk meg. 5. Ez három független áramkörök: a melegítő kör, és az anód áramkör a mágnesszelep áramkör. Az áramforrás lámpa egy két kenotron egyenirányító. szolenoid áramkör áramellátását külön szelén egyenirányító. Ra és reosztátot voltmérő anódfeszültsége Va megmarad. Az anód áramát mérik milliammeter mA. A jelenlegi a mágnesszelep áramkör azt állapítja meg a nagysága a mágneses mező által meghatározott reosztát Rs2 ampermérőt Ac.
1. megismertesse a berendezés és a telepítés az összeállított áramkör. Az ár meghatározására az egyes egységek megosztottság.
2. Kapcsolja be a tápegységet.
3. Kapcsolja be (kapcsoló „hálózat”) tápegységek.
4. Melegítsük a katód 2-3 percig.
5. Adjon Ua1 anódfeszültsége (Ua2) összhangban az említett táblázatban. 1 kiviteli alak szerint a univerzális tápegység.
7. Vegye ki a lefúvatási jellemzőkkel épített a grafikonok formájában szükségszerűen milliméterpapíron.
Egy tipikus formája a kiürített lefúvató jellemzőkkel ábrán látható. 6. Látható, hogy a görbe áll öt területen. Ez a különbség a ábra. 3. annak a ténynek köszönhető, hogy az elektronok elosztva a termikus sebességek, így.
Ezen túlmenően, a lámpa 2C 2C, a munkához használt, nem egy hengert alkot, és a kupakot. A henger az alsó (ábra. 7). Ennélfogva azon túlmenően, elektronok „keresztirányú”, azaz a mozog a keresztirányú síkban a magnetron, vannak elektronok hosszanti, azaz párhuzamosan mozog a tengellyel, vagy valamilyen szöget bezáróan (ábra. 7a).
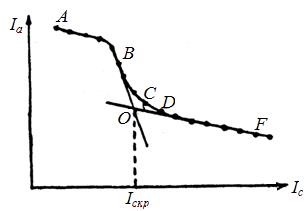
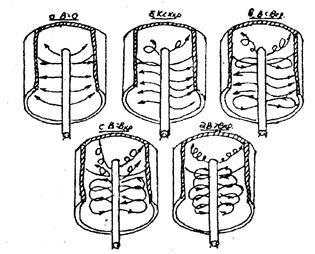
Ábra. 6. lemerült iszaptalanítói jellemzők Típus ábra. 7
A mozgás az elektronok a magnetron
Nézzük a jelenség megfelelő különböző részein a görbe (6. ábra):
1. A stroke rész B<Вкр объясняется тем, что электроны, вылетающие с торца катода, сильно закручивается полем (рис.7 б), т.к. радиус кривизны тем меньше, чем меньше поперечная скорость. В результате образуется пространственный заряд, ослабляющий поле вблизи торца катода и уменьшающий анодный ток в направлении донышка. С ростом В этот заряд должен расти и уменьшать ток Ua .
2. Amikor a <Вкр . но близкой к ней, часть «поперечных» электронов, имеющих максимальные тепловые скорости, закручиваются настолько, что не попадает на анод (участок В ). Это и есть начало «сброса» (рис. 7в).
3. Ugyanakkor, a növekedés az ilyen elektronok növekvő közel a hengeres része a katód van kialakítva egy tértöltés, amely kiszorítja az elektronok közel a katód homlokfelület, alja felé. Ennek eredményeként a csökkenés a jelenlegi kevésbé meredek (C rész).
4. kellően magas mező B> Bcr anód éri csak hosszanti emittált elektronok végétől. A mezők növekedése megnöveli a tértöltés vége (ld. 1.) és a fokozatos csökkenése a jelenlegi (F szakasz lemerült leiszapolás jellemzőit, ábra. 7d).
5. Plot D egy átmeneti rész a C részen F. A lényeges szerepet a számítás ezért bemutatott vita alapján a jelenlegi és a része a D és F az átmeneti területén a területen a C és D jelenléte miatt a „cool” elektronok.
Ezért, a kereszteződés a kiterjesztések részek B és F (O pont ábrán. 6) megfelel a megszüntetését érintkeznek az anóddal a „lassú” „keresztirányú” elektronok, azaz a Az ilyen termikus sebessége közel nulla (= O). Ez az állapot, mint az alapját a származtatása általános képletű (15). Ezért Ic találkozik Iskr áram az O pont (ábra. 7d).
Megtalálása a kereszteződés részek B és F. csökkentette merőlegesen az O pont az abszcisszán és meghatározzuk Iskr.
A kritikus mágneses mező indukció általános képletű:
Ezután, a (15) képletű kiszámításakor értékei e / m, és megállapította, azok számtani átlagértéke. A hiba értéke e / m határozzuk meg egy általános módszert, képlet alapján (15). Pontosság értékek la, lc. Ua szerint hozott pontossági osztály az eszköz. 2TS2S paraméterek és a hiba az alábbiakban: a = (0,095 ± 0,001) cm, a = (0,95 ± 0,01) cm K = (0,014 ± 0,001) T / a
1. Mi az a konkrét díjat az elektron?
2. Melyek a mérési módszerei fajlagos töltésének tudja?
3. Mi az úgynevezett magnetron? Hogyan működik?
4. Milyen erők hatnak az elektron mozgást a magnetron és irányította?
5. Mi az a kritikus mágneses mező?
7. Számított képlet meghatározására külön díj az elektron magnetron által?
8. Hogyan magyarázza az eltérést a kísérleti és elméleti jellemzőit hibája?
9. Mi a típusú és minőségű precíziós elektromos mérőműszerek ebben a vizsgálatban alkalmazott? A működési elve az eszköz?
10. Mi az oka (amellett berendezésekkel kapcsolatos hibák) hibákat okozhat a meghatározás?
1. Fizikai praktikus. „Villamos energia és optika.” VI Iverova, "Science", 1968, p. 321.
2. "Elektromosság". SG Kalasnyikov. "Science", 1964-ben, § 98, pp. 201-205.
3. A tanfolyam a fizika. BM Jaworski és munkatársai., "High iskola", 1964-ben, t. II, ch. XVII, § 18,1, 18,8, 18,4, 18,5.
4. A tantárgy az általános fizika. G.A.Zisman és OM Todes. M. "Science", 1965, Vol. II, Sec. VIII, §36, 37.