Körkörös mozdulatokkal, ez a fizika
Ω szögsebessége a test ezen a ponton az úgynevezett kör alakú nyomvonal határértékek (AT At → 0) a aránya a kis szögelfordulás δφ a kis időintervallum At:
Szögsebesség mérjük rad / s.
A kommunikáció a modul és a lineáris sebesség υ szögsebessége ω:
Az egyenletes mozgás a test kerülete υ és ω értékek változatlanok maradnak. Ebben az esetben a mozgás vektor megváltoztatja az irányt
Egységes mozgás a test kerület menti mozgás gyorsulás. gyorsulás
sugárirányban közepe felé a kör. Ez az úgynevezett normális vagy centripetális gyorsulás. Modul centripetális gyorsulás kapcsolatos υ lineáris és szögsebessége ω kapcsolatok:
Ennek bizonyítására nézzük a változás a kifejezés a sebességvektor egy kis ideig dt. A definíció szerint a gyorsulás
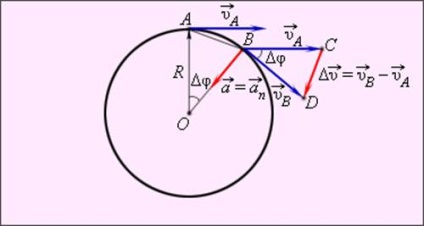
Centripetális gyorsulása a test egy egyenletes körmozgás
Velocity vektorok és az A és B pontok mentén vannak a kör érintője ezeken a pontokon. modulok egyenlő sebességek υA = υB = υ.
A hasonlóság a háromszögek OAB-hez és BCD (. Ábra 1.6.2) kell lennie:
A kis szögek esetén δφ = ωδt távolság | AB | = Δs ≈ υδt. Mivel | OA | = R | CD | = Δυ, a hasonlósága háromszögek ábrán. 1.6.2 kapjuk:
Abban a kis szögek δφ vektor irányában közelíti az irányt a közepén a kör. Így halad a határt, dt → 0, megkapjuk:
Ha megváltoztatja a testhelyzet a kör megváltoztatja az irányt a közepén a kör. A egyenletes mozgás a test kerülete mentén gyorsulás modul változatlan marad, de az irányt a gyorsulásvektor időben változik. Gyorsulásvektor bármely ponton a kör felé irányul közepén. Ezért, egyenletes gyorsulás mozgás a test kerülete mentén az úgynevezett centripetális.
Vektor formában a centripetális gyorsulás felírható
ahol - a sugár vektor egy pontot a kör kerületén, az elején, amely a közepén.
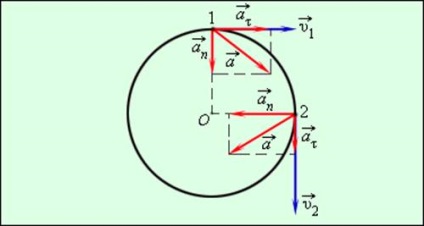
Ha a test mozog egyenetlen kört, majd ott is tangens (vagy érintőleges) komponense gyorsulás (lásd 1.1):
Ebben a képletben δυτ = υ2 - υ1 - változik a sebesség a modul alatt dt időintervallum.
Irányban teljes gyorsulásvektor meghatározzuk minden pontján a kör alakú nyomvonal értékeit normális és a tangenciális gyorsulások (ábra. 1.6.3).