Kihívások a hasonlóság háromszögek
Vegyünk néhány feladatot a hasonlóság háromszögek.
I. A háromszög tartott szegmens párhuzamos oldalsó. végpontjai a másik oldalán a háromszög.
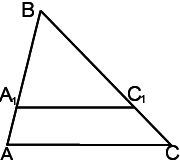
Tekintsük háromszögek ABC és A1BC1.
Problémák megoldása hasonló háromszögek segítségével kényelmesen színvisszaadás, ezért válassza ki az adatokat háromszögek különböző színekben:
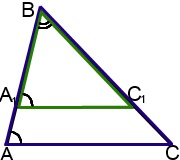
1) ∠ B - összesen;
2) ∠ BAC = ∠ BA1C1 (mint a megfelelő szögek a AC ∥ A1C1 és metsző AB).
Következésképpen, az ABC és A1BC1 háromszög hasonló (két sarkok).
A hasonlóság a háromszögek, hogy arányos legyen a megfelelő oldalai:
A vonal párhuzamos a AC oldal az ABC háromszög metszi az AB oldalt a ponton A1 és az irányt a nap - a ponton a B1. Find a hossza a szegmens A1C1, ha AC = 35, AA1: A1B = 2: 5.
Megmutatjuk, hasonlóságára háromszögek ABC és A1BC1.
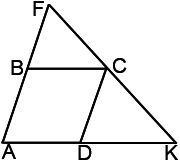
Tekintsük a háromszög AFK BFC.
Válassza ki az adatokat a színes háromszög.
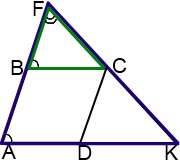
1) ∠ F - összesen;
2) ∠ FAK = ∠ FBC (mint a megfelelő szögek AD ∥ BC és metsző AB).
Következésképpen, a háromszög hasonló AFK és BFC (két sarkok).
A hasonlóság a háromszögek, hogy arányos legyen a megfelelő oldalai:
A rombusz beírt háromszög AFK ABCD úgy, hogy a szög, amelynél a teljes a C csúcsból tartozik FK oldalán. Keresse az irányt a rombusz, ha az AF = 21 cm, AK = 24 cm.
AFK bizonyítják a hasonlóság háromszögek és BFC. A három kapcsolatokról választani azokat, amelyek tudunk valamit:
Vesszük az oldalán a rombusz x:
Ezután BF = AF-AB = 21 cm-x. Ennélfogva,
Elosztjuk mindkét oldalán 3, megkapjuk:
A következő alkalommal, hogy a problémákat a hasonló háromszögek trapéz.