Képletek kiszámításához tömege üreges testek különböző formájú, matematika ékszerészek
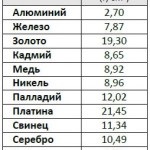
Soha nem fárad ismétlődő, hogy a test tömege - az térfogatának szorozva annak sűrűsége az anyag (lásd a táblázatot a sűrűségek.):
Azonban abban az esetben, üreges vagy üreges részt, akkor nem kell foglalkozni a hangerőt a testét, és a mennyiség falai. Displacement falai az üreges elem legegyszerűbb képviseletében a különbség a két térfogatú szilárd testek: külső méretek és a belső (a teljes test térfogata a belső üregek térfogata kivonjuk).
A képlet a térfogata a szilárd testek megtalálható a cikk „tömege a szilárd részek.”
Megjegyzés. Minden alábbi képletekben méretek milliméterben mérik, és a sűrűség - gramm per köbcentiméter.
Letter jelöli az arány a kerülete és átmérőjének aránya körülbelül 3,14.
1. A tömeg a cső (üreges henger)
A kötet a cső falak, ahol - a külső átmérője a cső, - a hossza a cső - falvastagság.
Miután egyszerűsítés megkapjuk a képlet a kötet:
Ezután a tömeg a cső:
2. Tömeg üreges (üreges) gömb
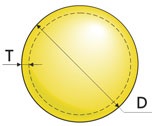
Aztán a tömeg:
3. A súlya üreges gömb szegmens
Elmozdulása a labda szegmens falak: ahol - a külső átmérője a bázis szegmens, - elevációval - falvastagság *.
Miután egyszerűsítés megkapjuk a képlet a kötet:
Aztán a tömeg:
4. A súlya egy üreges csonka kúp
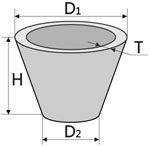
Miután egyszerűsítés megkapjuk a képlet a kötet:
Aztán a tömeg:
5. A súly egy üreges csonka
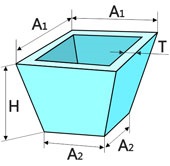
Miután egyszerűsítés megkapjuk a képlet a kötet:
Aztán a tömeg:
* Ebben az esetben - ez nem egészen a falvastagság. Szigorúan véve, van dolgunk két érték: az egyik, hogy áll a képletek a konzol, éppen a falvastagság, és az egyik, hogy vegye el a kívülről a testméret, hogy ez belső méretét - a falvastagság és a koszinusz hányadosa szög képző. De a legtöbb esetben, a falvastagság nem haladja meg a néhány százaléka a méret a test, és a hiba elhanyagolható. Azonban a vastag falú alkatrészek ezt a körülményt figyelembe kell venni.
Hasonló bejegyzések